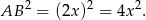Zadanie nr 1471381
Wierzchołki  i
i  kwadratu
kwadratu  leżą na paraboli
leżą na paraboli 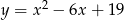 , przy czym odcinek
, przy czym odcinek 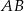 jest równoległy do osi
jest równoległy do osi 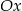 . Wykaż, że jeżeli odległość punktu
. Wykaż, że jeżeli odległość punktu 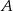 od osi
od osi  jest liczbą całkowitą to pole kwadratu
jest liczbą całkowitą to pole kwadratu  również jest liczbą całkowitą.
również jest liczbą całkowitą.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
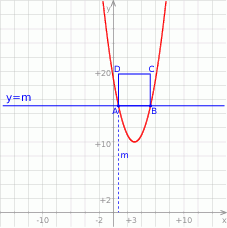
Sposób I
Powiedzmy, że wierzchołki 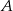 i
i 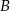 mają współrzędne
mają współrzędne 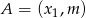 i
i 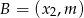 . Zatem punkty
. Zatem punkty 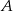 i
i 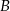 są punktami wspólnymi danej paraboli i prostej
są punktami wspólnymi danej paraboli i prostej 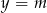 . To oznacza, że liczby
. To oznacza, że liczby 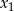 i
i 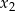 są pierwiastkami równania
są pierwiastkami równania
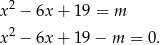
Obliczenie 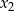 i
i 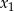 nie jest zbyt przyjemne, ale my nie potrzebujemy tych liczb – potrzebne nam jest tylko pole kwadratu, czyli
nie jest zbyt przyjemne, ale my nie potrzebujemy tych liczb – potrzebne nam jest tylko pole kwadratu, czyli
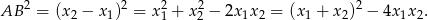
Teraz wystarczy skorzystać ze wzorów Viète’a.
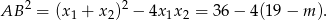
Teraz widać, że jeżeli 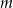 jest liczbą całkowitą, to całkowite jest też pole kwadratu
jest liczbą całkowitą, to całkowite jest też pole kwadratu 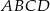 .
.
Sposób II
Zauważmy, że pierwsza współrzędna danej paraboli jest równa
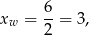
więc prosta 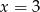 jest osią symetrii paraboli będącej jej wykresem. W takim razie punkty
jest osią symetrii paraboli będącej jej wykresem. W takim razie punkty 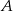 i
i 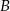 mają współrzędne postaci:
mają współrzędne postaci: 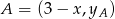 i
i 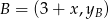 . Ponadto
. Ponadto
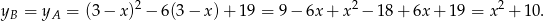
Z założenia wiemy, że 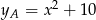 jest liczbą całkowitą, więc całkowita jest też liczba
jest liczbą całkowitą, więc całkowita jest też liczba 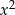 oraz
oraz