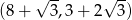Zadanie nr 1478761
W okrąg o równaniu 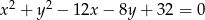 wpisano trójkąt równoboczny
wpisano trójkąt równoboczny 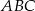 w którym
w którym 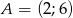 . Oblicz współrzędne pozostałych wierzchołków trójkąta.
. Oblicz współrzędne pozostałych wierzchołków trójkąta.
Rozwiązanie
Przekształćmy najpierw podane równanie okręgu.
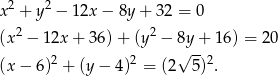
Możemy teraz naszkicować opisaną sytuację.
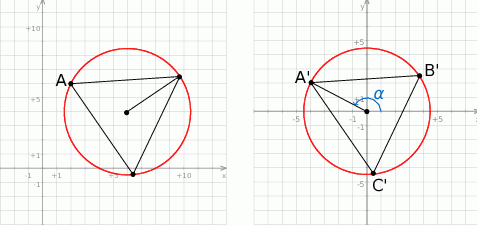
Sposób I
Jeżeli przez  oznaczymy długość boku szukanego trójkąta równobocznego, to promień okręgu opisanego na tym trójkącie to
oznaczymy długość boku szukanego trójkąta równobocznego, to promień okręgu opisanego na tym trójkącie to 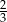 wysokości, czyli
wysokości, czyli
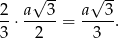
Mamy zatem
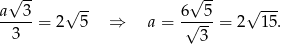
Szukamy zatem punktów 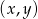 , które leżą na danym okręgu i których odległość od
, które leżą na danym okręgu i których odległość od 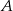 wynosi
wynosi 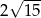 . Mamy więc układ równań
. Mamy więc układ równań
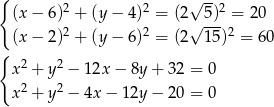
Odejmując te równania stronami mamy
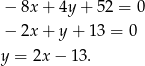
Podstawimy teraz wyliczoną wartość 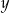 do równania okręgu
do równania okręgu
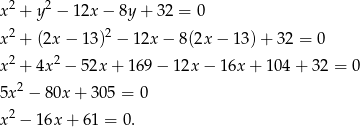
Liczymy dalej 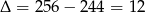 ,
,
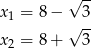
Wtedy
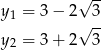
Sposób II
Tym razem rozpoczynamy od uproszczenia opisanej sytuacji – przesuwamy interesujące nas figury o wektor ![[− 6,− 4]](https://img.zadania.info/zad/1478761/HzadR16x.gif) tak, aby dany okrąg miał środek w punkcie
tak, aby dany okrąg miał środek w punkcie 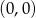 . Po tym przesunięciu punkt
. Po tym przesunięciu punkt 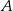 przejdzie w
przejdzie w 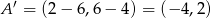 . Wszystkie punkty otrzymanego okręgu mają współrzędne postaci
. Wszystkie punkty otrzymanego okręgu mają współrzędne postaci 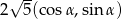 . Rozpocznijmy od obliczenia funkcji trygonometrycznych kąt
. Rozpocznijmy od obliczenia funkcji trygonometrycznych kąt  , dla którego otrzymujemy punkt
, dla którego otrzymujemy punkt 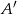 .
.
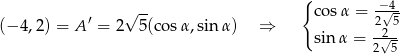
Współrzędne pozostałych wierzchołków 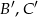 trójkąta równobocznego otrzymamy obracając punkt
trójkąta równobocznego otrzymamy obracając punkt 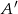 o
o 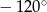 i o
i o 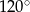 . Zanim obliczymy współrzędne tych punktów zauważmy, że
. Zanim obliczymy współrzędne tych punktów zauważmy, że
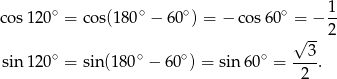
Mamy zatem
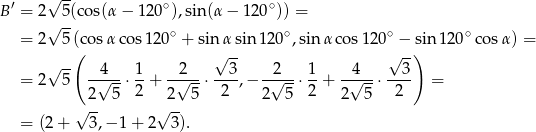
Analogicznie obliczamy współrzędne punktu 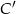 .
.
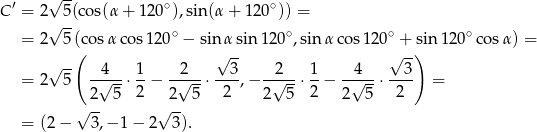
Współrzędne punktów 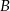 i
i 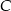 otrzymujemy przesuwając punkty
otrzymujemy przesuwając punkty 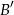 i
i 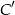 o wektor
o wektor ![[6,4]](https://img.zadania.info/zad/1478761/HzadR36x.gif) . Mamy zatem
. Mamy zatem
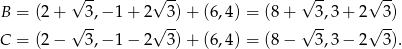
Odpowiedź: 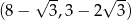 ,
,