Zadanie nr 2361045
Dany jest okrąg o równaniu 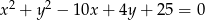 . Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
. Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
Rozwiązanie
Aby narysować opisaną sytuację, przekształćmy podane równanie okręgu tak, aby było widać jaki jest jego środek i promień.
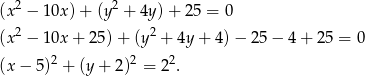
Jest to więc okrąg o środku 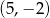 i promieniu
i promieniu 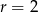 .
.
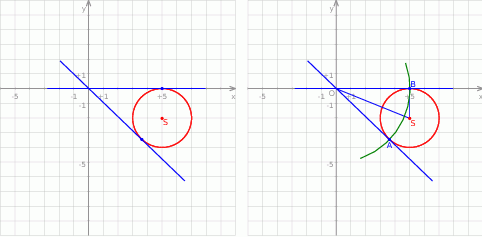
Sposób I
Proste przechodzące przez początek układu współrzędnych są postaci 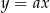 dla pewnego
dla pewnego  (tak naprawdę jest jeszcze pionowa prosta
(tak naprawdę jest jeszcze pionowa prosta 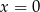 , która nie jest tej postaci, ale widać, że ona nie jest styczną). Sprawdźmy kiedy prosta
, która nie jest tej postaci, ale widać, że ona nie jest styczną). Sprawdźmy kiedy prosta 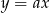 ma dokładnie jeden punkt wspólny z podanym okręgiem (podstawiamy
ma dokładnie jeden punkt wspólny z podanym okręgiem (podstawiamy 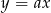 do równania okręgu).
do równania okręgu).
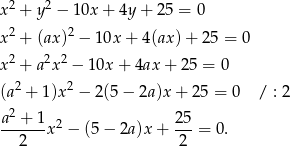
Skoro otrzymane równanie kwadratowe ma mieć dokładnie jeden pierwiastek, to jego 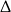 musi być równa 0 (spodziewając się tego podzieliliśmy równanie stronami przez 2, żeby otrzymać prostszą
musi być równa 0 (spodziewając się tego podzieliliśmy równanie stronami przez 2, żeby otrzymać prostszą 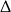 -ę).
-ę).
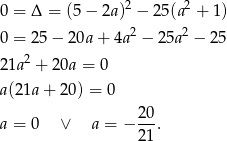
Sposób II
Tym razem użyjemy odrobinę więcej geometrii. Z obrazka widać, że jedną z szukanych stycznych jest prosta 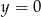 – łatwo to sprawdzić, okrąg ma środek
– łatwo to sprawdzić, okrąg ma środek 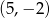 i promień
i promień 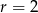 , więc jest styczny do tej prostej. To oznacza, że znamy odległość początku układu współrzędnych od interesujących nas punktów styczności:
, więc jest styczny do tej prostej. To oznacza, że znamy odległość początku układu współrzędnych od interesujących nas punktów styczności: 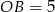 (gdybyśmy nie zauważyli styczności
(gdybyśmy nie zauważyli styczności 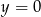 i okręgu, moglibyśmy wyliczyć
i okręgu, moglibyśmy wyliczyć 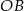 z trójkąta prostokątnego
z trójkąta prostokątnego 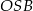 ).
).
Zatem punkty styczności 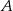 i
i 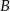 są punktami wspólnymi danego okręgu i okręgu
są punktami wspólnymi danego okręgu i okręgu 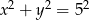 (o środku w
(o środku w 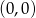 i promieniu 5). Mamy więc układ równań
i promieniu 5). Mamy więc układ równań
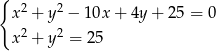
Odejmujemy od pierwszego równania drugie (żeby skrócić kwadraty) i mamy
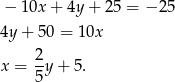
Podstawiamy to do równania drugiego okręgu i mamy
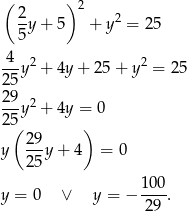
Pierwsza wartość 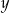 daje znany już nam punkt
daje znany już nam punkt 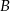 , więc zajmijmy się drugą. Mamy wtedy
, więc zajmijmy się drugą. Mamy wtedy
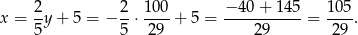
Zatem 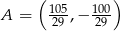 i pozostało ustalić dla jakiego
i pozostało ustalić dla jakiego  prosta
prosta 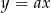 przechodzi przez ten punkt. Mamy
przechodzi przez ten punkt. Mamy
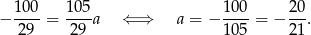
Sposób III
Tym razem tak jak w pierwszym sposobie szukamy stycznej w postaci 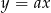 , ale zamiast przecinać ją z okręgiem sprawdźmy, kiedy jest ona odległa od środka okręgu
, ale zamiast przecinać ją z okręgiem sprawdźmy, kiedy jest ona odległa od środka okręgu 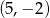 o długość promienia
o długość promienia 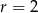 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 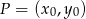 od prostej
od prostej 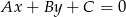 :
:
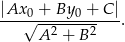
W naszej sytuacji (dla prostej 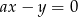 ) otrzymujemy równanie
) otrzymujemy równanie
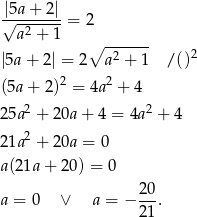
Odpowiedź: 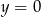 i
i