/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 2452624

Dodaj do ulubionych
Dodaj do rozwiązanych

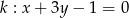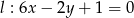Znajdź równanie prostej, zawierającą dwusieczną tego kąta, utworzonego przez proste k : x + 3y − 1 = 0 oraz l : 6x − 2y+ 1 = 0 , do obszaru którego należy punkt P (3,1) .

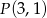Rozwiązanie

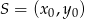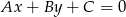Korzystamy ze wzoru na odległość punktu S = (x0,y0) od prostej Ax + By + C = 0 :

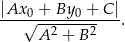
|Ax-0√-+-By-0 +-C|. A 2 + B 2

Dwusieczna to zbiór punktów równo odległych od obu prostych czyli zbiór punktów postaci

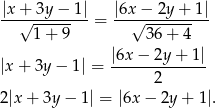
|x-+-3y-−-1| |6x−--2y-+-1| √ 1+--9- = √ 36-+-4- |x + 3y − 1| = |6x-−-2y-+-1-| 2 2|x + 3y − 1| = |6x − 2y + 1|.

Zbiór opisany tym równaniem to tak naprawdę obie dwusieczne. Jeżeli chcemy je rozdzielić to musimy opuścić wartości bezwzględne. Sprawdźmy jakie są znaki wyrażeń pod wartościami bezwzględnymi w interesującym nas obszarze: podstawiamy do tych wyrażeń współrzędne punktu 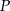P . Jak wstawimy to okaże się, że oba są dodatnie, czyli opuszczamy wartości bezwzględne bez zmiany znaku.

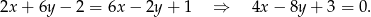
2x+ 6y − 2 = 6x − 2y + 1 ⇒ 4x − 8y + 3 = 0.

Na koniec obrazek.

PIC

 
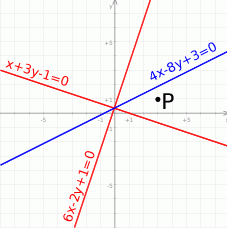
Odpowiedź: 4x − 8y + 3 = 0

Wersja PDF