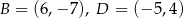Zadanie nr 2566303
Punkty 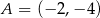 i
i 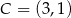 są wierzchołkami rombu
są wierzchołkami rombu 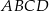 , którego wierzchołek
, którego wierzchołek 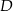 leży na prostej
leży na prostej 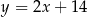 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 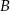 i
i 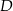 .
.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
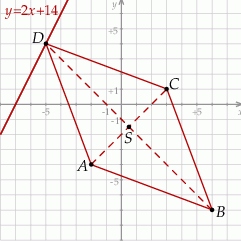
Obliczamy współrzędne punktu przecięcia się przekątnych rombu.
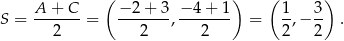
Sposób I
Szukamy punktu 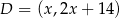 , który leży na prostej
, który leży na prostej 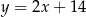 i jest który jest równoodległy od punktów
i jest który jest równoodległy od punktów 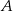 i
i 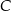 .
.
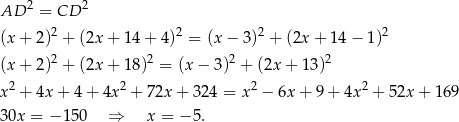
Stąd 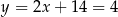 i
i 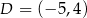 . Współrzędne wierzchołka
. Współrzędne wierzchołka 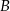 wyznaczamy korzystając z tego, że
wyznaczamy korzystając z tego, że 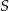 jest środkiem odcinka
jest środkiem odcinka 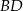 .
.
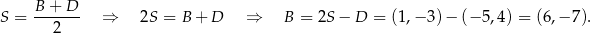
Sposób II
Tym razem napiszemy równanie symetralnej odcinka 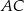 (czyli przekątnej
(czyli przekątnej 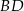 ) i znajdziemy jej punkt wspólny
) i znajdziemy jej punkt wspólny 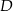 z daną prostą. Równanie prostej
z daną prostą. Równanie prostej 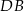 napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora
napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/2566303/HzadR17x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 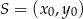 :
:
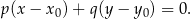
W naszej sytuacji mamy
![→ → v = AC = [5,5]](https://img.zadania.info/zad/2566303/HzadR20x.gif)
i 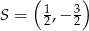 . Zatem prosta
. Zatem prosta  ma równanie
ma równanie
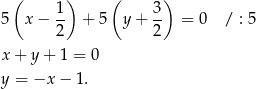
Szukamy teraz punktu wspólnego prostej  i danej prostej
i danej prostej 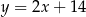 . Podstawiamy w tym drugim równaniu
. Podstawiamy w tym drugim równaniu 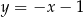 .
.
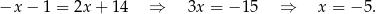
Stąd 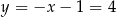 i
i 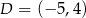 . Współrzędne punktu
. Współrzędne punktu 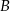 wyznaczamy tak samo jak w poprzednim sposobie.
wyznaczamy tak samo jak w poprzednim sposobie.
Odpowiedź: