/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 2572171

Dodaj do ulubionych
Dodaj do rozwiązanych

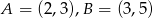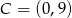Dane są punkty A = (2,3),B = (3,5) i C = (0 ,9) . Wyznacz współrzędne punktu 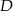D , dla którego czworokąt 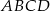ABCD jest trapezem prostokątnym, którego kąt przy wierzchołku 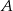A jest prosty.

Rozwiązanie

Rozpoczynamy od schematycznego rysunku.

PIC

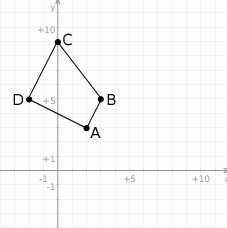
Skoro bok 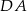DA ma być prostopadły do 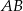AB i widać, że bok 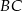BC nie jest prostopadły do 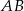AB , to podstawami trapezu muszą być boki 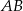AB i CD .

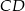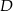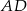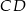Współrzędne punktu D wyznaczymy pisząc równania prostych AD i CD – pierwsza z nich jest prostopadła, a druga równoległa do 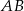AB . Zanim to jednak zrobimy napiszmy równanie prostej 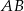AB (potrzebny nam jest jej współczynnik kierunkowy).

Szukamy prostej w postaci 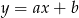y = ax+ b i podstawiamy współrzędne punktów 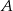A i B .

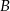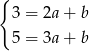
{ 3 = 2a + b 5 = 3a + b

Odejmując od drugiego równania pierwsze mamy 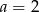a = 2 . No i dalej możemy nie liczyć, bo potrzebny nam był tylko współczynnik kierunkowy.

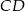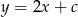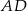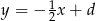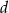W takim razie prosta CD ma postać y = 2x + c , a prosta AD postać y = − 12x + d . Współczynniki c i d wyznaczamy podstawiając współrzędne odpowiednio punktów 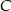C i A .

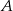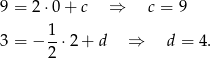
9 = 2⋅ 0+ c ⇒ c = 9 1 3 = − --⋅2 + d ⇒ d = 4. 2

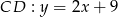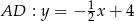Pozostało znaleźć punkt wspólny prostych CD : y = 2x + 9 i 1 AD : y = − 2x + 4 .

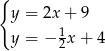
{ y = 2x + 9 y = − 12x + 4

Porównując 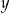y -ki mamy

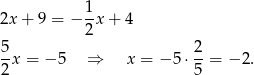
1- 2x+ 9 = − 2 x+ 4 5 2 -x = − 5 ⇒ x = − 5 ⋅--= − 2. 2 5

Zatem 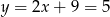y = 2x + 9 = 5 i D = (− 2,5) .  
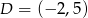Odpowiedź: D = (− 2,5)

Wersja PDF