Zadanie nr 5521273
Przedłużenia ramion 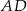 i
i 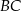 trapezu równoramiennego
trapezu równoramiennego 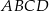 przecinają się w punkcie
przecinają się w punkcie 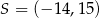 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 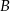 i
i 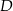 tego trapezu, jeżeli
tego trapezu, jeżeli 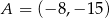 i
i 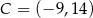 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
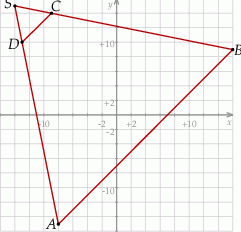
Sposób I
Wiemy, że trapez jest równoramienny, więc
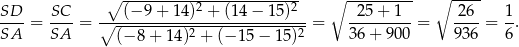
To pozwala łatwo wyznaczyć współrzędne wierzchołków 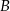 i
i 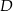 . Najpierw wierzchołek
. Najpierw wierzchołek 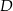 .
.
![−S→D = 1-−S→A = 1[6,− 30] = [1,− 5] 6 6 −→ D = S + SD = (− 1 4,15)+ [1 ,− 5 ] = (− 13 ,10).](https://img.zadania.info/zad/5521273/HzadR5x.gif)
Teraz wierzchołek 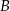 .
.
![−→ −→ SB = 6SC = 6[5,− 1] = [30,− 6] −→ B = S + SB = (− 14,15 )+ [30,− 6] = (16,9 ).](https://img.zadania.info/zad/5521273/HzadR7x.gif)
Sposób II
Tym razem spróbujemy obejść się bez wektorów. Piszemy najpierw równanie prostej 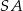 . Szukamy prostej w postaci
. Szukamy prostej w postaci 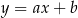 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 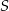 i
i 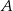 .
.
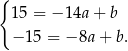
Odejmujemy od pierwszego równania drugie i mamy
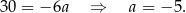
Stąd 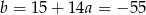 i prosta
i prosta 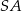 ma równanie
ma równanie 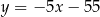 . Szukamy teraz na tej prostej punktu
. Szukamy teraz na tej prostej punktu 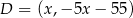 takiego, że
takiego, że
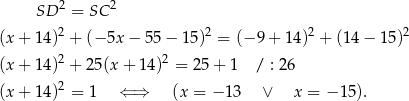
Łatwo zauważyć, że jeżeli 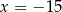 , to punkty
, to punkty 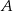 i
i 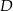 są po różnych stronach punktu
są po różnych stronach punktu 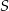 , co nie jest możliwe. Zatem
, co nie jest możliwe. Zatem 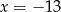 ,
, 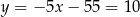 i
i 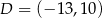 .
.
Zupełnie analogicznie możemy wyznaczyć współrzędne punktu 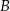 , ale dla urozmaicenia zrobimy to inaczej – wyznaczymy
, ale dla urozmaicenia zrobimy to inaczej – wyznaczymy 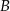 jako punkt wspólny prostych
jako punkt wspólny prostych 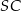 i
i 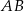 . Piszemy najpierw równanie prostej
. Piszemy najpierw równanie prostej 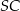 – szukamy prostej w postaci
– szukamy prostej w postaci 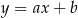 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów  i
i 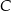
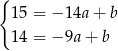
Odejmujemy od drugiego równania pierwsze i mamy
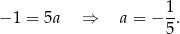
Stąd  i prosta
i prosta 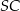 ma równanie
ma równanie 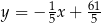 .
.
Współczynnik kierunkowy prostej 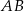 jest taki sam jak współczynnik kierunkowy prostej
jest taki sam jak współczynnik kierunkowy prostej 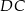 , czyli jest równy
, czyli jest równy
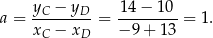
Prosta 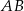 ma więc równanie postaci
ma więc równanie postaci 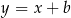 . Współczynnik
. Współczynnik  obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu 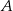 .
.

Prosta 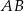 ma więc równanie
ma więc równanie 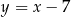 . Pozostało wyznaczyć jej punkt wspólny
. Pozostało wyznaczyć jej punkt wspólny 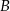 z prostą
z prostą 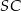 . Podstawiamy
. Podstawiamy 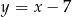 w równaniu prostej
w równaniu prostej 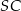 .
.
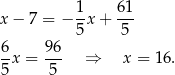
Stąd 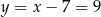 i
i 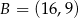 .
.
Odpowiedź: 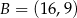 ,
, 

