Zadanie nr 9806015
Ciągiem Fibonacciego nazywamy ciąg, którego dwa pierwsze wyrazy są równe 1, a każdy kolejny jest sumą dwóch poprzednich. Jaką liczbą, parzystą czy nieparzystą, jest 528 wyraz ciągu Fibonacciego? Odpowiedź uzasadnij.
Rozwiązanie
Wypiszmy kilka początkowych wyrazów podanego ciągu
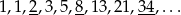
Widać pojawiającą się prawidłowość: parzyste wyrazy pojawiają się na miejscach podzielnych przez 3: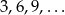 
(innymi słowy, co trzeci wyraz jest parzysty). Nie jest trudno tę obserwację uzsadnić, na początku mamy dwie liczby nieparzyste, ich suma jest więc parzysta. Następnie dostaniemy znowu dwie liczby nieparzyste (jako sumy liczby parzystej i nieparzystej) itd.
Ponieważ 528 dzieli się przez 3 (suma cyfr jest równa 15), to odpowiedni wyraz ciągu Fibonacciego jest liczbą parzystą.
Odpowiedź: Jest to liczba parzysta.
