Zadanie nr 9592466
Wszystkie liczby parzyste z przedziału 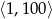 , które nie są podzielne przez 4 ustawiamy w ciąg
, które nie są podzielne przez 4 ustawiamy w ciąg 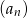 .
.
- Wyznacz wzór ciągu
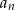 i uzasadnij, że jest on arytmetyczny.
i uzasadnij, że jest on arytmetyczny. - Oblicz sumę wszystkich wyrazów tego ciągu.
Rozwiązanie
- Liczby o których mowa to
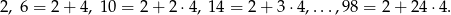
Widać więc, że jest to ciąg arytmetyczny o różnicy 4 i wzorze ogólnym
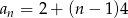
Odpowiedź: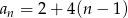
- Z poprzedniego podpunktu wiemy, że wszystkich wyrazów ciągu
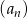 jest 25. Zatem
jest 25. Zatem 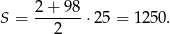
Odpowiedź: 1250

