Rozwiąż nierówność 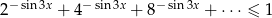 , gdzie
, gdzie 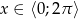 .
.
/Szkoła średnia/Nierówności
Udowodnij, że jeżeli 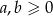 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 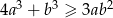 .
.
Wykaż, że dla dowolnych nieujemnych liczb rzeczywistych  ,
, 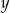 spełniona jest nierówność:
spełniona jest nierówność: 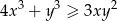 .
.
Uzasadnij, że jeżeli 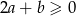 , to
, to 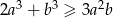 .
.
Udowodnij, że jeśli 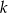 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 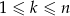 , to
, to 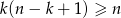 .
.
Rozwiąż nierówność 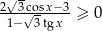 w przedziale
w przedziale 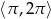 .
.
Rozwiązaniem nierówności 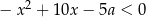 jest zbiór
jest zbiór 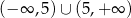 . Wyznacz
. Wyznacz  .
.
Wykaż, że jeżeli 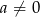 i
i 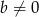 , to
, to 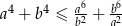 .
.
Rozwiąż nierówność
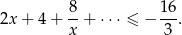
Rozwiąż nierówność, której lewa strona jest sumą szeregu geometrycznego
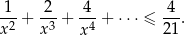
Zaznacz w układzie współrzędnych zbiór punktów 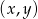 , dla których współrzędne spełniają nierówność
, dla których współrzędne spełniają nierówność 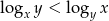 .
.
Rozwiąż nierówność 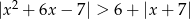 .
.
Wykaż, że dla dowolnej liczby 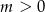 prawdziwa jest nierówność
prawdziwa jest nierówność 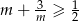 .
.
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 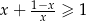 .
.
Udowodnij, że dla dowolnej dodatniej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
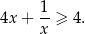
Udowodnij, że dla dowolnej ujemnej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
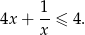
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 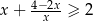 .
.
Posługując się wykresem funkcji 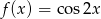 dla
dla 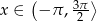 , rozwiąż nierówność
, rozwiąż nierówność 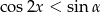 wiedząc, że miara kąta
wiedząc, że miara kąta  jest równa mierze łukowej kąta środkowego okręgu opartego na
jest równa mierze łukowej kąta środkowego okręgu opartego na 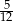 okręgu.
okręgu.
Wyznacz wszystkie wartości  , dla których nierówność
, dla których nierówność 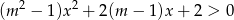 jest prawdziwa dla każdego
jest prawdziwa dla każdego 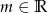 .
.
Rozwiąż nierówność 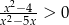 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 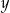 takich, że
takich, że 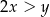 , spełniona jest nierówność
, spełniona jest nierówność
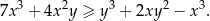
Rozwiąż nierówność 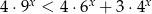 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 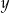 prawdziwa jest nierówność
prawdziwa jest nierówność
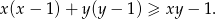
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 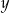 prawdziwa jest nierówność
prawdziwa jest nierówność
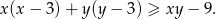
Rozwiąż nierówność 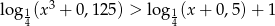 .
.
Wykaż, że jeżeli 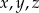 są długościami boków trójkąta to
są długościami boków trójkąta to 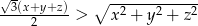 .
.
Wyznacz wszystkie wartości 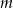 , dla których nierówność
, dla których nierówność 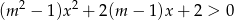 jest prawdziwa dla każdego
jest prawdziwa dla każdego 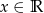 .
.
Rozwiąż nierówność 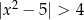 .
.

