Zadanie nr 1319614
Rozwiąż nierówność 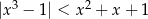 .
.
Rozwiązanie
Daną nierówność może zapisać w postaci
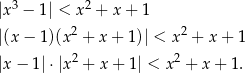
Zauważmy teraz, że
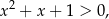
bo 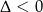 . W takim razie możemy obie strony nierówności podzielić stronami przez
. W takim razie możemy obie strony nierówności podzielić stronami przez 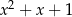 i zostaje nierówność
i zostaje nierówność
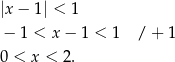
Odpowiedź: 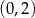
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 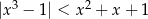 .
.
Daną nierówność może zapisać w postaci
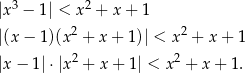
Zauważmy teraz, że
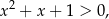
bo 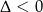 . W takim razie możemy obie strony nierówności podzielić stronami przez
. W takim razie możemy obie strony nierówności podzielić stronami przez 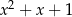 i zostaje nierówność
i zostaje nierówność
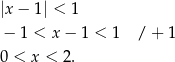
Odpowiedź: