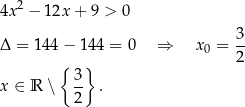Nierówność kwadratowa to nierówność postaci
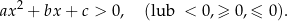
Przypomnijmy, że wykresem lewej strony takiej nierówności jest parabola, której ramiona są skierowane do góry dla 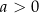 i w dół dla
i w dół dla 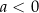 . Ponadto
. Ponadto
-
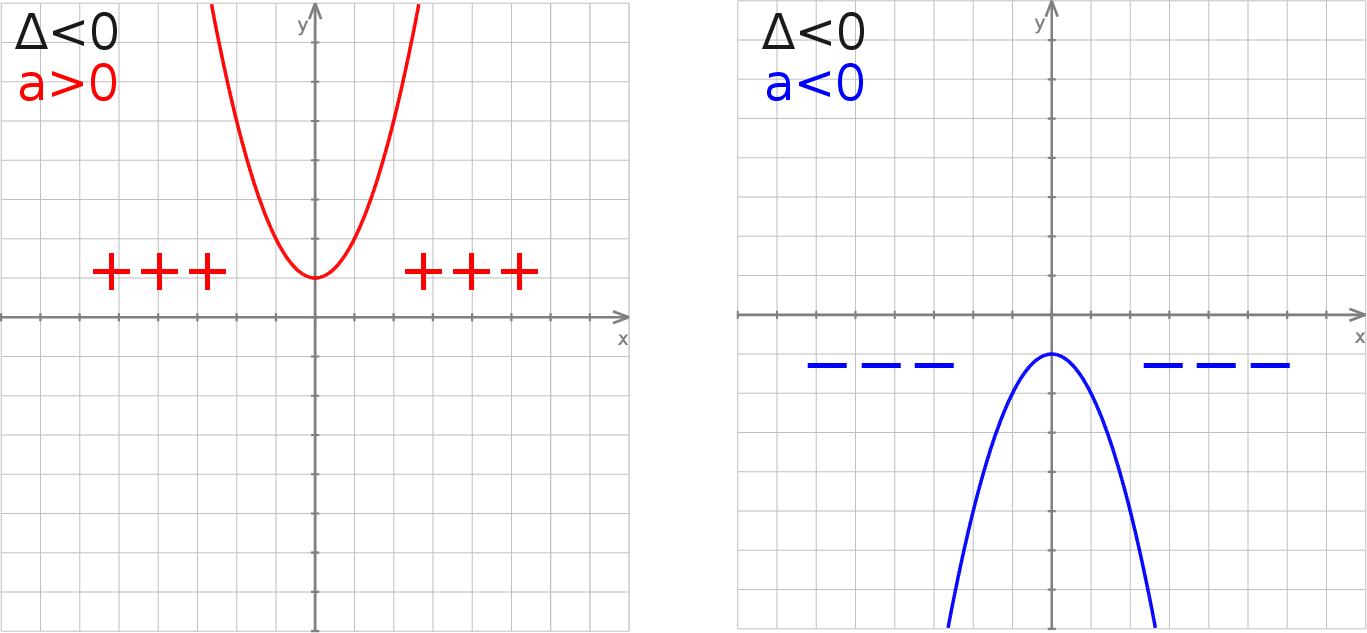
parabola nie przecina osi
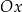 jeżeli
jeżeli 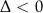 ;
; 
-
przecina oś
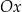 w jednym punkcie jeżeli
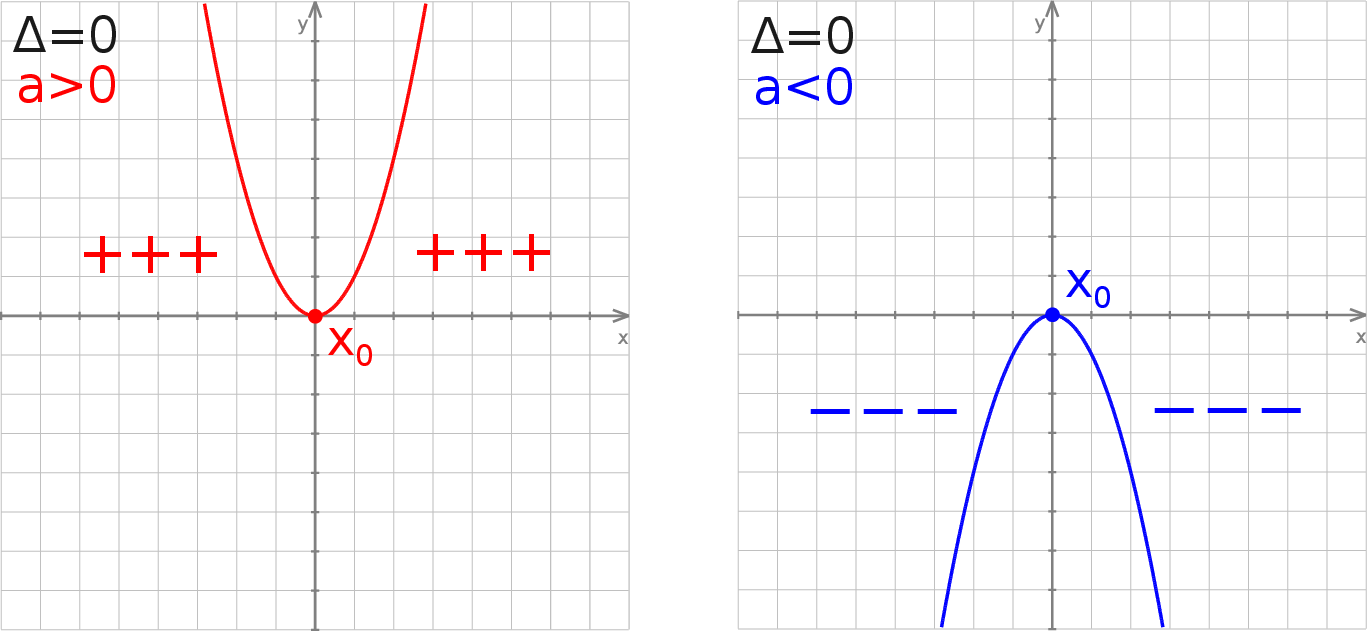
w jednym punkcie jeżeli 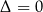 ;
; 
-
przecina oś
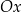 w dwóch punktach jeżeli
w dwóch punktach jeżeli 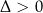 .
. 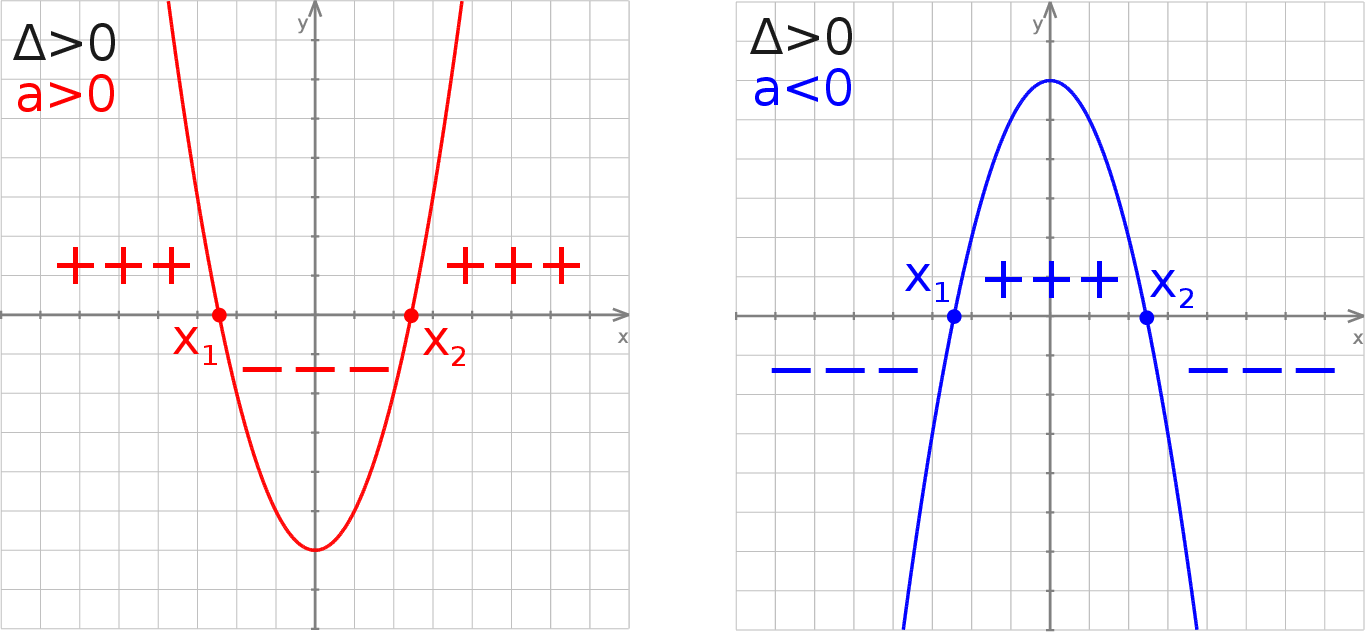
Patrząc na powyższe rysunki, bez trudu ustalamy znak wyrażenia  .
.
-
Jeżeli
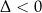 to wyrażenie
to wyrażenie 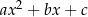 jest stale dodatnie dla
jest stale dodatnie dla 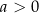 i ujemne dla
i ujemne dla 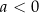 .
. -
Jeżeli
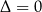 to wyrażenie
to wyrażenie 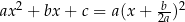 jest równe 0 dla
jest równe 0 dla 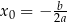 i jest dodatnie dla
i jest dodatnie dla 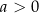 (ujemne dla
(ujemne dla 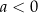 ) na zbiorze
) na zbiorze 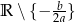 .
. -
Jeżeli
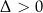 i
i 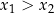 są pierwiastkami, to wyrażenie
są pierwiastkami, to wyrażenie 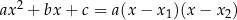 jest dodatnie dla
jest dodatnie dla 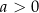 (ujemne dla
(ujemne dla 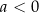 ) na zbiorze
) na zbiorze 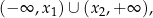
oraz ujemne dla
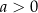 (dodatnie dla
(dodatnie dla 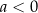 ) na zbiorze
) na zbiorze 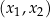 .
.
Nierówność
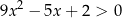
jest zawsze spełniona, gdyż 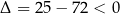 .
.
Jak to zapamiętać? Na pierwszy rzut oka można czuć się zagubionym w tych wszystkich przypadkach, ale grunt to nie uczyć się tego na pamięć, tylko wypracować system. Przede wszystkim, zawsze możemy nierówność sprowadzić do postaci z dodatnim współczynnikiem przy 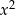 – można to łatwo zrobić mnożąc nierówność przez -1. Przy takim założeniu sprawa zaczyna być prosta.
– można to łatwo zrobić mnożąc nierówność przez -1. Przy takim założeniu sprawa zaczyna być prosta.
Funkcja kwadratowa jest ujemna między pierwiastkami i dodatnia na zewnątrz od pierwiastków.
W zasadzie to jest wszystko co trzeba pamiętać. Przypadki 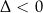 i
i 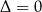 też podpadają pod tę formułkę – dla
też podpadają pod tę formułkę – dla 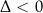 nie ma pierwiastków i funkcja jest cały czas dodatnia, a dla
nie ma pierwiastków i funkcja jest cały czas dodatnia, a dla 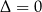 funkcja jest dodatnia na zewnątrz od jedynego pierwiastka.
funkcja jest dodatnia na zewnątrz od jedynego pierwiastka.
Spróbujmy rozwiązać nierówność
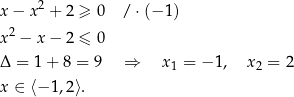
Rozwiążmy nierówność