Funkcje wykładnicze i logarytmiczne są ze sobą bardzo blisko związane i dlatego omówimy je w jednym poradniku. Funkcja wykładnicza Funkcją wykładniczą nazywamy funkcję postaci 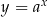 , gdzie
, gdzie 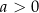 i
i 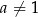 . Dziedziną funkcji wykładniczej jest cały zbiór liczb rzeczywistych.
. Dziedziną funkcji wykładniczej jest cały zbiór liczb rzeczywistych.
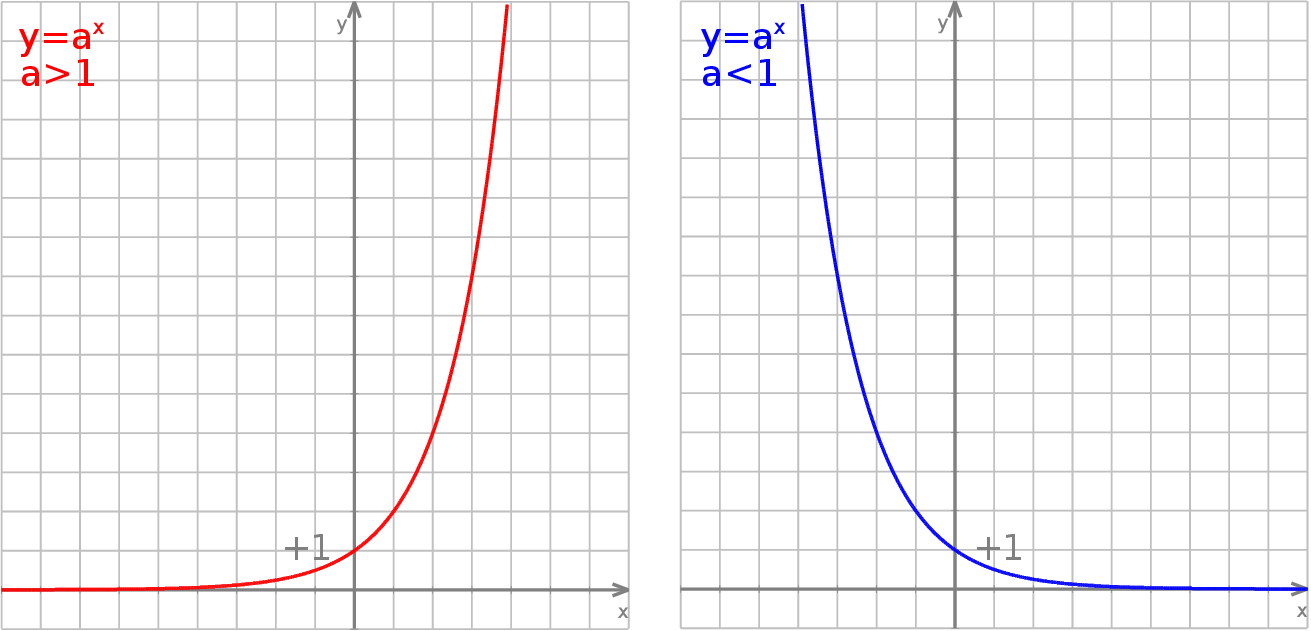
Jeżeli 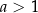 to funkcja wykładnicza jest rosnąca i rośnie od 0 do
to funkcja wykładnicza jest rosnąca i rośnie od 0 do 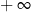 . Jeżeli natomiast
. Jeżeli natomiast 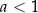 , to funkcja jest malejąca i maleje od
, to funkcja jest malejąca i maleje od 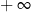 do 0.
do 0.
W obu przypadkach wykres funkcji wykładniczej przecina oś 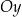 w punkcie
w punkcie 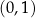 . Funkcja logarytmiczna Funkcją logarytmiczną nazywamy funkcję postaci
. Funkcja logarytmiczna Funkcją logarytmiczną nazywamy funkcję postaci 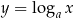 , gdzie
, gdzie  jest ustaloną liczbą dodatnią i
jest ustaloną liczbą dodatnią i 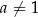 . Dziedziną funkcji logarytmicznej jest zbiór liczb dodatnich.
. Dziedziną funkcji logarytmicznej jest zbiór liczb dodatnich.
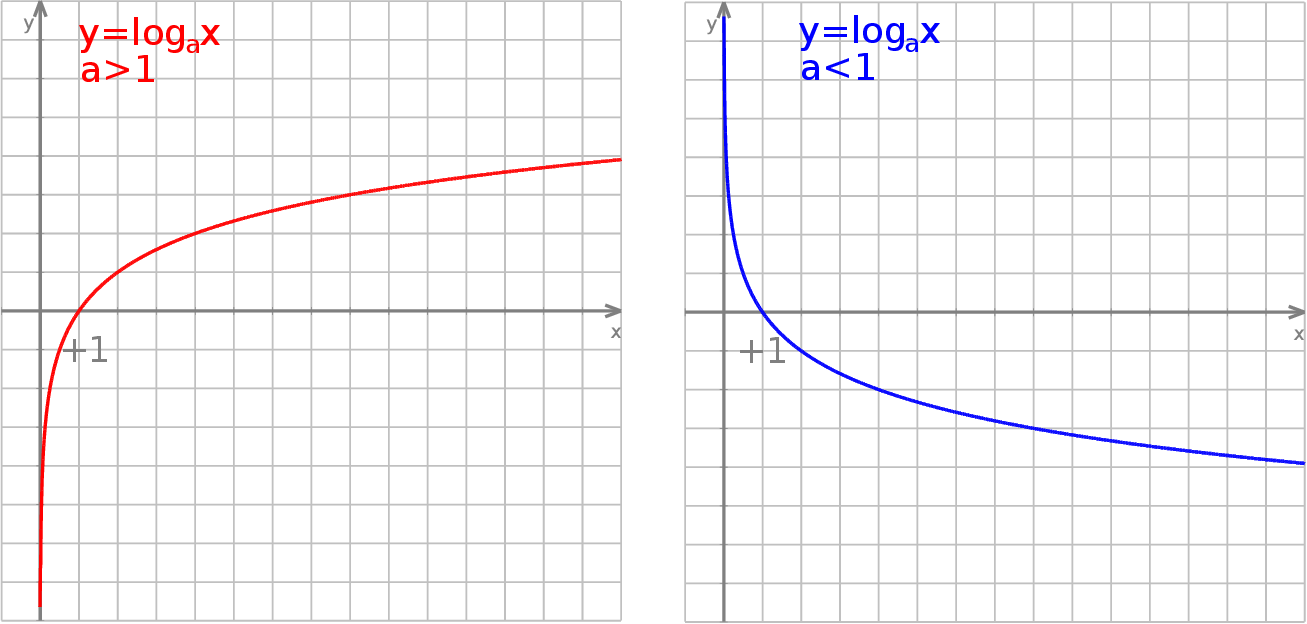
Dla  funkcja
funkcja  jest funkcją rosnącą i rośnie od
jest funkcją rosnącą i rośnie od 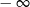 do
do 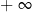 . Dla
. Dla 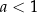 funkcja
funkcja 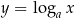 jest funkcją malejącą i maleje od
jest funkcją malejącą i maleje od 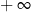 do
do  .
.
W obu przypadkach wykres funkcji logarytmicznej przecina oś 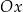 w punkcie
w punkcie 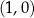 . Związek funkcji wykładniczej z funkcją logarytmiczną Funkcja logarytmiczna
. Związek funkcji wykładniczej z funkcją logarytmiczną Funkcja logarytmiczna 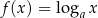 jest funkcją odwrotną do funkcji wykładniczej
jest funkcją odwrotną do funkcji wykładniczej 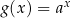 , tzn.
, tzn.
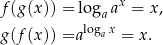
O funkcji odwrotnej należy myśleć tak: jeżeli traktujemy funkcję 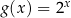 jako maszynkę, która zamienia liczbę
jako maszynkę, która zamienia liczbę  na liczbę
na liczbę 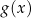 , czyli 2 na 4, 4 na 16, 10 na 1024 itd., to funkcja odwrotna
, czyli 2 na 4, 4 na 16, 10 na 1024 itd., to funkcja odwrotna 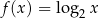 zamienia te liczby w drugą stronę: 4 na 2, 16 na 4, 1024 na 10.
zamienia te liczby w drugą stronę: 4 na 2, 16 na 4, 1024 na 10.
Na wykresie ten związek przejawia się symetrią: wykresy funkcji 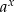 i
i 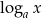 są symetryczne względem prostej
są symetryczne względem prostej 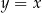 .
.
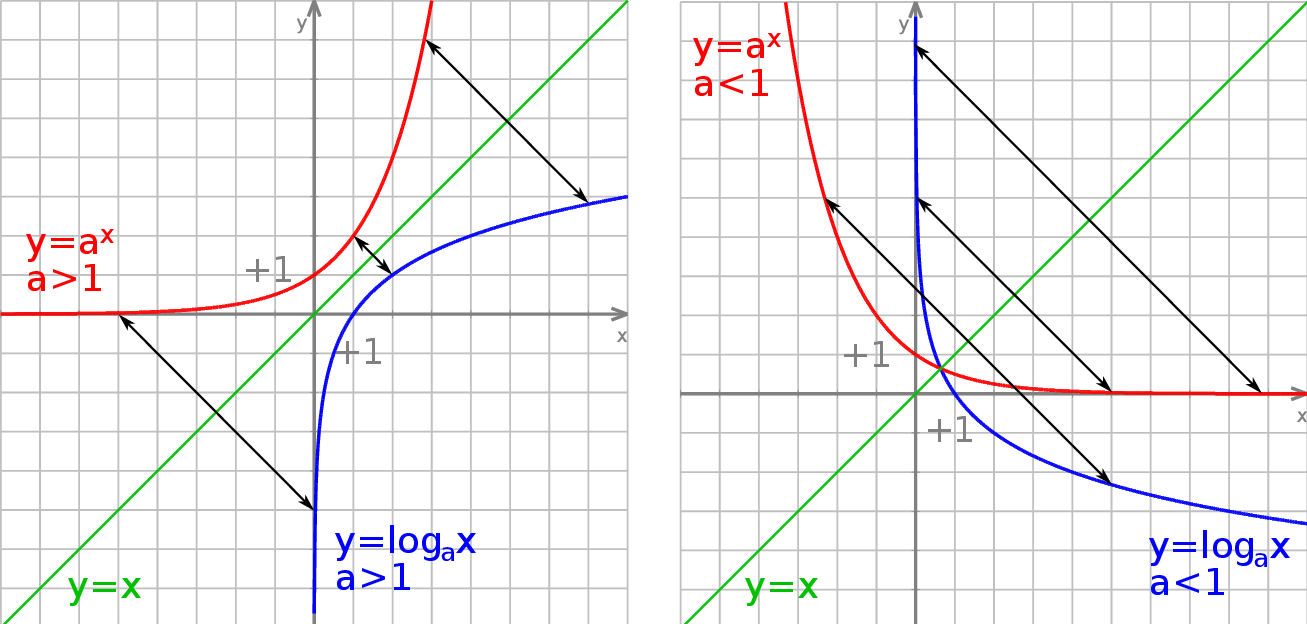
Jeżeli popatrzymy na wykres logarytmu to widać, że logarytm rośnie/maleje (w zależności od  ) na początku szybko (powiedzmy do
) na początku szybko (powiedzmy do 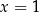 ), a potem bardzo wolno. Odpowiada to temu, że funkcja wykładnicza rośnie/maleje wolno dla
), a potem bardzo wolno. Odpowiada to temu, że funkcja wykładnicza rośnie/maleje wolno dla 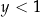 i bardzo szybko dla
i bardzo szybko dla 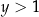 .
.

