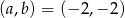/Szkoła średnia/Równania/Układy równań/Liniowy/Z parametrem

Zadanie nr 9364170

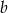Wyznacz takie liczby a i b , dla których układ równań 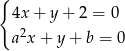{ 4x + y+ 2 = 0 a 2x+ y+ b = 0 jest sprzeczny, zaś układ równań 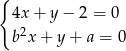{ 4x + y − 2 = 0 b2x + y + a = 0 ma nieskończenie wiele rozwiązań.

Wersja PDF

Rozwiązanie

Jeżeli układ równań

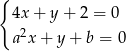
{ 4x + y + 2 = 0 a2x + y + b = 0

ma być sprzeczny, to proste opisane równaniami układu muszą być równoległe i różne. Tak jest jeżeli 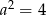2 a = 4 i b ⁄= 2 .

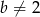Patrzymy teraz na drugi układ równań

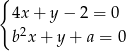
{ 4x + y − 2 = 0 b2x + y + a = 0

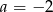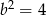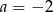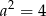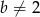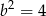Jeżeli ma on mieć nieskończenie wiele rozwiązań, to proste opisane równaniami układu muszą się pokrywać. Tak jest, gdy a = − 2 i 2 b = 4 . Zauważmy, że a = − 2 spełnia warunek a2 = 4 , a warunki b ⁄= 2 i b2 = 4 oznaczają, że b = − 2 .  
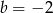Odpowiedź: (a,b) = (− 2,− 2)

Wersja PDF