Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 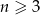 wyraża się wzorem
wyraża się wzorem 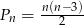 .
.
- Oblicz liczbę przekątnych w dwudziestokącie wypukłym.
- Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
- Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
- Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.

 o boku długości
o boku długości  . Wiedząc, że
. Wiedząc, że 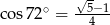
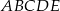 jest równa
jest równa 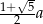 ;
; 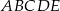 .
.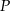 , będący punktem wewnętrznym trójkąta
, będący punktem wewnętrznym trójkąta 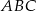 , przekształcamy przez symetrię względem prostych zawierających boki
, przekształcamy przez symetrię względem prostych zawierających boki 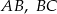 i
i 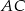 otrzymując odpowiednio punkty
otrzymując odpowiednio punkty 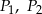 i
i 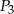 . Udowodnij, że pole sześciokąta
. Udowodnij, że pole sześciokąta 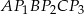 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 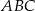 .
. 
 . Udowodnij, że przekątna pięciokąta foremnego o boku długości 1 ma długość
. Udowodnij, że przekątna pięciokąta foremnego o boku długości 1 ma długość 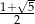 .
. 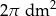 . Oblicz pole powierzchni wielokąta.
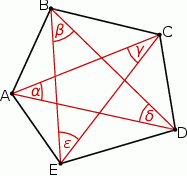
. Oblicz pole powierzchni wielokąta. 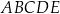 jest wpisany w okrąg. Przekątne
jest wpisany w okrąg. Przekątne 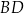 i
i 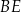 tego pięciokąta przecinają przekątną
tego pięciokąta przecinają przekątną 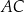 w punktach
w punktach 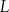 i
i  odpowiednio (zobacz rysunek).
odpowiednio (zobacz rysunek). 
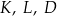 i
i 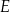 leżą na jednym okręgu, to
leżą na jednym okręgu, to 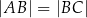 .
.  bokach.
bokach. 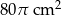 , oblicz:
, oblicz: 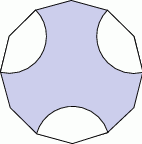
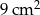 . Oblicz pole koła opisanego na tym sześciokącie.
. Oblicz pole koła opisanego na tym sześciokącie. 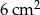 . Oblicz pole koła opisanego na tym sześciokącie.
. Oblicz pole koła opisanego na tym sześciokącie.  –kąta foremnego jest o
–kąta foremnego jest o 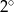 mniejsza od miary kąta wewnętrznego
mniejsza od miary kąta wewnętrznego 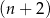 – kąta foremnego. Oblicz
– kąta foremnego. Oblicz  .
.  –kąta foremnego jest o
–kąta foremnego jest o 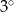 mniejsza od miary kąta wewnętrznego
mniejsza od miary kąta wewnętrznego 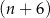 – kąta foremnego. Oblicz
– kąta foremnego. Oblicz  .
.  –kąta foremnego jest o 73 mniejsza niż liczba przekątnych
–kąta foremnego jest o 73 mniejsza niż liczba przekątnych 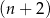 –kąta. Oblicz
–kąta. Oblicz  .
. 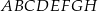 o boku długości 1.
o boku długości 1. 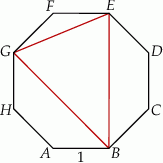
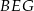 jest równe
jest równe 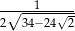 .
.  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru 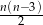 , gdzie
, gdzie 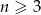 ,
, 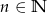 . Ile boków ma wielokąt, który ma 35 przekątnych?
. Ile boków ma wielokąt, który ma 35 przekątnych? 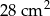 . Oblicz pola tych wielokątów.
. Oblicz pola tych wielokątów.  –kąta wypukłego jest równa
–kąta wypukłego jest równa 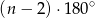 .
.  –kącie foremnym, gdzie
–kącie foremnym, gdzie 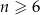 , iloczyn liczby najdłuższych przekątnych przez liczbę najkrótszych przekątnych jest o 342 większy niż liczba osi symetrii tego wielokąta. Oblicz
, iloczyn liczby najdłuższych przekątnych przez liczbę najkrótszych przekątnych jest o 342 większy niż liczba osi symetrii tego wielokąta. Oblicz  .
. 