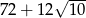Zadanie nr 6770571
Podstawą ostrosłupa 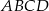 jest trójkąt
jest trójkąt 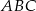 , a krawędź
, a krawędź 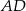 jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa
jest wysokością ostrosłupa. Oblicz pole powierzchni całkowitej ostrosłupa 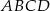 , jeśli wiadomo, że jego objętość jest równa 48 oraz
, jeśli wiadomo, że jego objętość jest równa 48 oraz 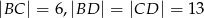 . Podaj wszystkie możliwe odpowiedzi.
. Podaj wszystkie możliwe odpowiedzi.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
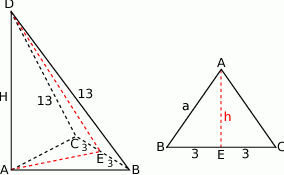
Jeżeli oznaczymy długość wysokości ostrosłupa przez 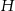 to z trójkątów prostokątnych
to z trójkątów prostokątnych 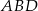 i
i 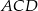 mamy
mamy

W szczególności trójkąt 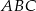 jest równoramienny i jego wysokość ma długość
jest równoramienny i jego wysokość ma długość
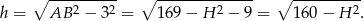
Możemy teraz wykorzystać podaną objętość ostrosłupa.
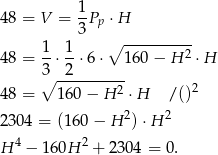
Otrzymaliśmy równanie dwukwadratowe, więc podstawmy 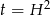 .
.
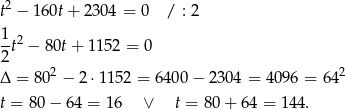
Daje to nam odpowiednio 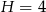 i
i 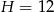 (bo
(bo 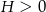 ).
).
Pozostało obliczyć pole powierzchni całkowitej ostrosłupa (w każdym z przypadków). Żeby nie liczyć dwa razy tego samego, policzymy je dla dowolnego 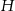 , a na koniec podstawimy wyliczone wyżej wartości.
, a na koniec podstawimy wyliczone wyżej wartości.
Pola trzech ścian liczymy ’od ręki’
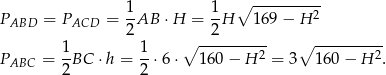
Teraz liczymy wysokość ściany 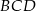 z trójkąta prostokątnego
z trójkąta prostokątnego 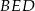 (można też z
(można też z 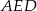 )
)
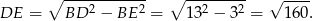
Zatem
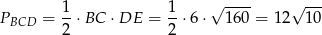
i pole powierzchni całkowitej ostrosłupa jest równe
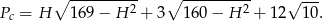
Podstawiając 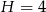 i
i 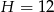 otrzymujemy odpowiednio
otrzymujemy odpowiednio
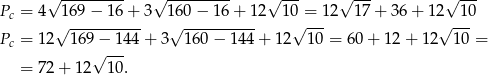
Odpowiedź: 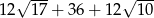 lub
lub