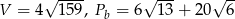/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworościan

Zadanie nr 7580518

Podstawą ostrosłupa jest trójkąt równoramienny o ramieniu długości 10 i podstawie długości 12. Wszystkie krawędzie boczne ostrosłupa mają długość 7. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

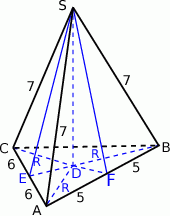
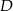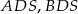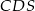Niech D będzie spodkiem wysokości ostrosłupa. Zauważmy, że każdy z trójkątów ADS ,BDS i CDS jest prostokątny z przyprostokątną długości 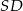SD i przeciwprostokątną długości 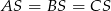AS = BS = CS . Trójkąty te są więc przystające, czyli 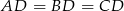AD = BD = CD . To oznacza, że punkt 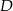D jest środkiem okręgu opisanego na trójkącie ABC .

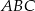Obliczmy teraz promień 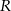R okręgu opisanego na trójkącie 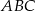ABC . Można to zrobić ze wzoru na pole 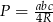P = abc 4R , ale my zrobimy to bardziej wprost, z twierdzenia sinusów.

Obliczmy najpierw długość wysokości podstawy

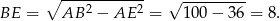
∘ ----2------2 √ --------- BE = AB − AE = 100 − 36 = 8 .

Liczymy promień okręgu opisanego.

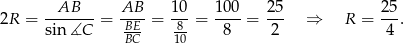
AB AB 10 100 25 2 5 2R = -------= BE--= -8-= ----= --- ⇒ R = ---. sin ∡C BC- 10 8 2 4

Możemy teraz obliczyć długość wysokości ostrosłupa – patrzymy na trójkąt prostokątny 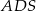ADS .

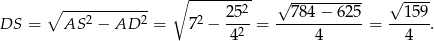
∘ --------- √ ---------- √ ---- ∘ ------------ 252 784 − 62 5 1 59 DS = AS 2 − AD 2 = 72 − --2-= ------------ = ------. 4 4 4

Możemy teraz obliczyć objętość ostrosłupa

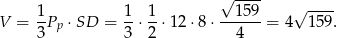
√ ---- ---- V = 1P ⋅SD = 1-⋅ 1-⋅12 ⋅8 ⋅-159-= 4√ 159 . 3 p 3 2 4

Aby obliczyć pole powierzchni bocznej musimy najpierw obliczyć wysokości ścian bocznych. Zacznijmy od 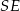SE .

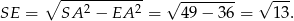
------------ ∘ 2 2 √ -------- √ --- SE = SA − EA = 49− 36 = 13 .

Obliczmy pole trójkąta 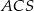ACS .

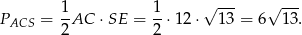
1 1 √ --- √ --- PACS = -AC ⋅SE = --⋅12 ⋅ 13 = 6 13. 2 2

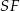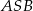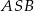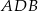Niech teraz SF będzie wysokością ściany ASB . Zauważmy, że trójkąty ASB i ADB są równoramienne, więc punkt 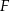F jest środkiem krawędzi 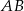AB . Zatem

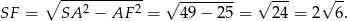
∘ ------------ √ -------- √ --- √ -- SF = SA 2 − AF 2 = 49 − 25 = 2 4 = 2 6.

Liczymy pole trójkąta 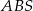ABS .

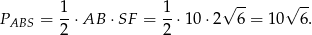
1- 1- √ -- √ -- PABS = 2 ⋅AB ⋅SF = 2 ⋅10 ⋅2 6 = 10 6.

Pole powierzchni bocznej jest więc równe

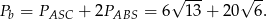
√ --- √ -- P = P + 2P = 6 13 + 20 6. b ASC ABS

 
Odpowiedź: √ ---- √ --- √ -- V = 4 15 9, Pb = 6 13+ 20 6

Wersja PDF