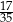Zadanie nr 4614018
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta utworzonego przez dwie sąsiednie ściany boczne.
Rozwiązanie
Zaczynamy oczywiście od dużego rysunku.

Musimy najpierw ustalić jak obliczyć kąt między ścianami bocznymi. Ogólnie, taki kąt wyznacza się przecinając kąt dwuścienny płaszczyzną prostopadłą do krawędzi kąta i liczy się miarę otrzymanego kąta płaskiego. W naszej sytuacji sprawa jest dość prosta. Jeżeli poprowadzimy wysokości 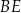 i
i 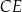 w trójkątach ścian bocznych, opuszczone na krawędź
w trójkątach ścian bocznych, opuszczone na krawędź 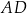 , to ponieważ ostrosłup jest prawidłowy (ściany są przystające), to spodki tych wysokości będą dokładnie w tym samym punkcie – oznaczmy go przez
, to ponieważ ostrosłup jest prawidłowy (ściany są przystające), to spodki tych wysokości będą dokładnie w tym samym punkcie – oznaczmy go przez 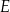 . Otrzymana płaszczyzna
. Otrzymana płaszczyzna 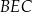 jest prostopadła do krawędzi
jest prostopadła do krawędzi 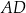 , zatem kąt
, zatem kąt 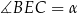 jest kątem między ścianami bocznymi.
jest kątem między ścianami bocznymi.
Cosinus szukanego kąta będziemy mogli obliczyć z twierdzenia cosinusów w trójkącie 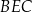 . Aby to zrobić, musimy obliczyć długości wysokości
. Aby to zrobić, musimy obliczyć długości wysokości 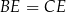 . Oznaczmy przez
. Oznaczmy przez  długość krawędzi podstawy ostrosłupa. Wtedy krawędź boczna ma długość
długość krawędzi podstawy ostrosłupa. Wtedy krawędź boczna ma długość 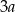 .
.
Narysujmy sobie z boku trójkąt 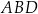 . Chcemy obliczyć jego wysokość
. Chcemy obliczyć jego wysokość 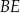 . Obliczymy najpierw z twierdzenia Pitagorasa wysokość
. Obliczymy najpierw z twierdzenia Pitagorasa wysokość 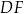
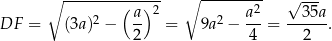
Porównajmy teraz dwa wzory na pole trójkąta 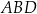 (inny sposób, to podobieństwo trójkątów
(inny sposób, to podobieństwo trójkątów 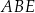 i
i 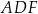 )
)
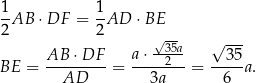
Pozostało zastosować twierdzenie cosinusów do trójkąta 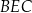 .
.
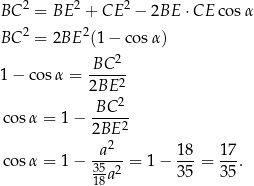
Odpowiedź: