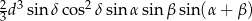/Szkoła średnia/Geometria/Stereometria/Ostrosłup

Zadanie nr 4998401

Dodaj do ulubionych
Dodaj do rozwiązanych

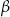Podstawą ostrosłupa jest trójkąt o danych kątach α i β . Wszystkie krawędzie boczne mają długość 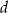d i są nachylone do płaszczyzny podstawy pod kątem o mierze 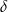δ . Oblicz objętość tego ostrosłupa.

Rozwiązanie

Jak to w zadaniach ze stereometrii zaczynamy od dużego rysunku.

PIC

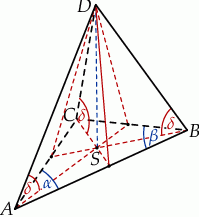
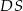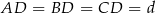Przyjmijmy oznaczenia z rysunku, tzn. niech DS będzie wysokością ostrosłupa, AD = BD = CD = d , ∡BAC = α , ∡ABC = β .

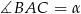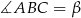Najważniejszą (i najtrudniejszą) rzeczą do zrobienia jest ustalenie, gdzie leży rzut wierzchołka D na płaszczyznę podstawy – jeżeli to ustalimy, to mając d i δ będziemy mogli zacząć liczyć długości odcinków w trójkącie ABC .

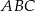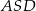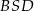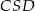Zauważmy, że trójkąty prostokątne ASD , BSD i CSD są przystające (mają dwa takie same boki). Zatem

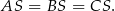
AS = BS = CS .

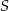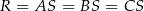Oznacza to, że S jest środkiem okręgu opisanego na trójkącie ABC . Niech R = AS = BS = CS . Z trójkąta prostokątnego 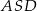ASD mamy

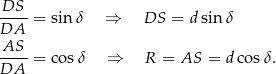
DS DA-- = sin δ ⇒ DS = d sin δ AS-- = cos δ ⇒ R = AS = d cosδ . DA

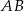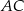Teraz, dzięki twierdzeniu sinusów, możemy obliczyć długości boków AB i AC trójkąta ABC .

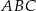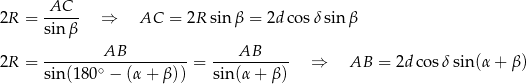
2R = AC--- ⇒ AC = 2R sin β = 2d cos δsin β sin β AB AB 2R = -------∘------------= ----------- ⇒ AB = 2d cos δsin(α + β) sin (180 − (α + β)) sin(α + β)

Pole trójkąta 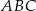ABC obliczamy ze wzoru z sinusem.

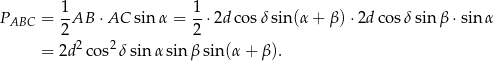
1 1 PABC = 2-AB ⋅AC sin α = 2 ⋅2d cos δsin(α + β )⋅2d cos δsinβ ⋅sin α 2 2 = 2d cos δ sinα sinβ sin(α + β).

Pozostało obliczyć objętość ostrosłupa

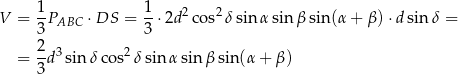
1- 1- 2 2 V = 3PABC ⋅ DS = 3 ⋅2d cos δ sinα sinβ sin(α + β) ⋅d sin δ = 2 = -d3sin δco s2δsin αsin βsin(α + β ) 3

 
Odpowiedź: 2d 3sinδ cos2δ sin α sin β sin(α + β) 3

Wersja PDF