Zadanie nr 2709020
Wyznacz pole trójkąta, którego dwa boki zawierają się w asymptotach wykresu funkcji 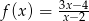 , a trzeci bok zawiera się w stycznej do wykresu tej funkcji w punkcie
, a trzeci bok zawiera się w stycznej do wykresu tej funkcji w punkcie 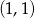 .
.
Rozwiązanie
Na początku musimy wyznaczyć te asymptoty i styczną. Ponieważ
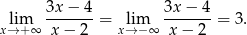
funkcja ta ma jedną asymptotę poziomą 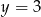 . Ponadto jest asymptota pionowa
. Ponadto jest asymptota pionowa 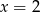 . Możemy teraz naszkicować wykres funkcji
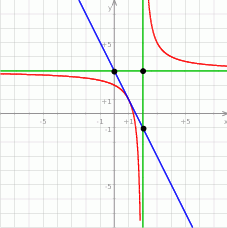
. Możemy teraz naszkicować wykres funkcji  .
.
Aby wyznaczyć styczną, liczymy pochodną
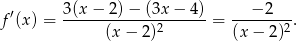
Zatem 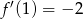 i styczna do wykresu w punkcie
i styczna do wykresu w punkcie 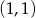 ma postać
ma postać 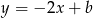 . Współczynnik
. Współczynnik 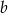 obliczamy z warunku, że punkt
obliczamy z warunku, że punkt 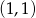 należy do wykresu.
należy do wykresu.

Ponieważ prosta 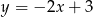 przecina proste
przecina proste 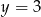 i
i 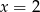 w punktach
w punktach 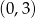 i
i 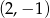 odpowiednio, interesujący nas trójkąt jest trójkątem prostokątnym o przyprostokątnych długości 2 i 4. Zatem ma pole
odpowiednio, interesujący nas trójkąt jest trójkątem prostokątnym o przyprostokątnych długości 2 i 4. Zatem ma pole
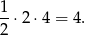
Odpowiedź: 4

