/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 4467549

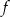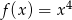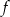Funkcja f jest określona wzorem 4 f(x ) = x dla każdej liczby rzeczywistej x . Wyznacz równanie prostej stycznej do wykresu funkcji f , która jest równoległa do prostej y = 4x + 7 .

Wersja PDF

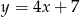Rozwiązanie

Musimy sprawdzić w jakim punkcie styczna do wykresu 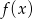f(x ) ma współczynnik kierunkowy równy 4. To pytanie, to dokładnie pytanie, w jakim punkcie pochodna przyjmuje wartość 4. Liczymy

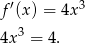
f′(x) = 4x 3 3 4x = 4.

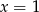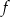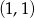Stąd x = 1 i odpowiadający punkt na wykresie funkcji f to (1,1) . Szukamy zatem prostej postaci 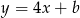y = 4x+ b przechodzącej przez punkt 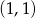(1,1) . Podstawiając współrzędne tego punktu do równania prostej mamy 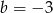b = − 3 , więc szukana styczna to y = 4x− 3 .

PIC

 
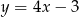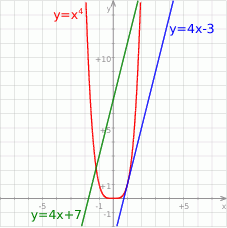
Odpowiedź: y = 4x− 3

Wersja PDF