/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 5678380

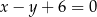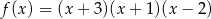Oblicz pole trójkąta utworzonego przez prostą x− y+ 6 = 0 , oś Ox oraz styczną do wykresu funkcji f(x) = (x + 3)(x + 1 )(x− 2) w punkcie o pierwszej współrzędnej x = − 2 .

Wersja PDF

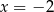Rozwiązanie

Obliczmy najpierw drugą współrzędną punktu, w którym mamy poprowadzić styczną do wykresu.

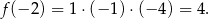
f(− 2) = 1 ⋅(− 1)⋅(− 4) = 4.

Aby obliczyć pochodną funkcji 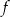f przekształcamy jej wzór.

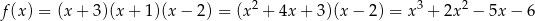
f(x ) = (x + 3)(x + 1)(x − 2) = (x2 + 4x+ 3)(x − 2) = x3 + 2x 2 − 5x − 6

Liczymy pochodną

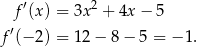
′ 2 f (x) = 3x + 4x − 5 f ′(− 2) = 12− 8− 5 = − 1.

Styczna do wykresu funkcji 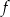f w punkcie 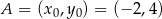A = (x 0,y0) = (− 2,4) ma więc równanie

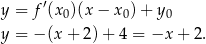
y = f ′(x0)(x − x 0)+ y 0 y = − (x + 2) + 4 = −x + 2 .

Szkicujemy teraz opisaną sytuację.

PIC

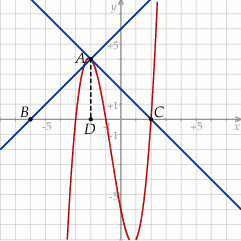
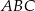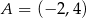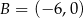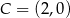W wykresu powinno być jasne, że mamy do czynienia z trójkątem ABC o wierzchołkach A = (−2 ,4) , B = (−6 ,0) i C = (2 ,0 ) . Wysokość 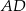AD tego trójkąta ma długość 4, a podstawa 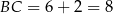BC = 6 + 2 = 8 . Jego pole jest więc równe

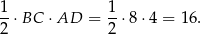
1 1 --⋅BC ⋅AD = --⋅8 ⋅4 = 16. 2 2

 
Odpowiedź: 16

Wersja PDF