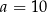/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Styczne do wykresu

Zadanie nr 6840274

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru a , dla których prosta 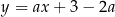y = ax + 3 − 2a jest styczna do wykresu funkcji 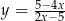y = 52−x4−x5- w punkcie o drugiej współrzędnej równej 3.

Rozwiązanie

Sprawdźmy dla jakiego argumentu x dana funkcja przyjmuje wartość 3.

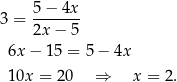
3 = 5-−-4x- 2x − 5 6x − 15 = 5− 4x 10x = 20 ⇒ x = 2 .

Liczymy pochodną funkcji

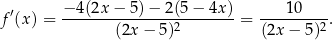
′ −-4(2x−--5)−--2(5−--4x)- ---10----- f (x) = (2x − 5)2 = (2x − 5)2.

Obliczamy wartość pochodnej w interesującym nas punkcie 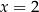x = 2 .

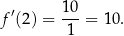
f ′(2 ) = 10-= 10. 1

W takim razie współczynnik kierunkowy stycznej w punkcie 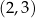(2,3) jest równy 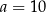a = 10 . Na koniec obrazek dla ciekawskich.

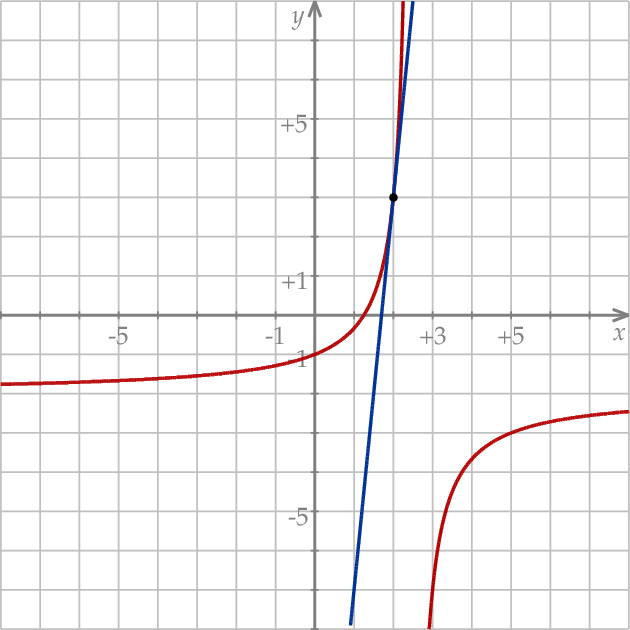
ZINFO-FIGURE

 
Odpowiedź: a = 1 0

Wersja PDF