Zadanie nr 2571470
Dana jest funkcja 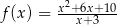 .
.
- Określ przedziały monotoniczności tej funkcji.
- Znajdź ekstrema lokalne funkcji
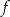 .
.
Rozwiązanie
- Korzystamy ze wzoru na pochodną ilorazu.
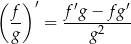
liczymy pochodną danej funkcji
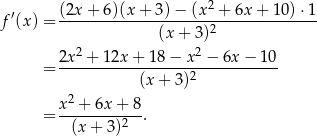
Aby wyznaczyć przedziały monotoniczności danej funkcji, musimy zbadać znak pochodnej. Mianownik jest dodatni (o ile
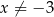 ), musimy zatem rozłożyć trójmian w liczniku.
), musimy zatem rozłożyć trójmian w liczniku. 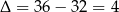 ,
, 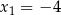 ,
, 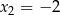 . Widzimy zatem, że licznik jest dodatni dla
. Widzimy zatem, że licznik jest dodatni dla 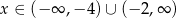 i ujemny dla
i ujemny dla 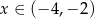 . Uwzględniając jeszcze fakt, że musi być
. Uwzględniając jeszcze fakt, że musi być 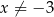 mamy
mamy 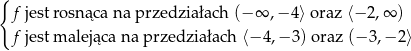
Odpowiedź: Rosnąca w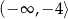 i
i 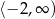 , malejąca w
, malejąca w 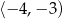 i
i 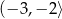 .
. - Z poprzedniego podpunktu wiemy, że miejsca zerowe pochodnej to
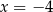 i
i 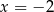 . Ponadto w pierwszym z tych punktów funkcja zmienia znak z ’+’ na ’-’, a w drugim odwrotnie. Zatem w
. Ponadto w pierwszym z tych punktów funkcja zmienia znak z ’+’ na ’-’, a w drugim odwrotnie. Zatem w 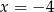 mamy maksimum lokalne, a w
mamy maksimum lokalne, a w 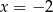 minimum lokalne. Odpowiadające wartości
minimum lokalne. Odpowiadające wartości 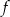 , to
, to 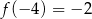 i
i 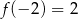 .
.
Odpowiedź: Minimum lokalne: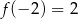 , maksimum lokalne:
, maksimum lokalne: 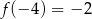 .
.
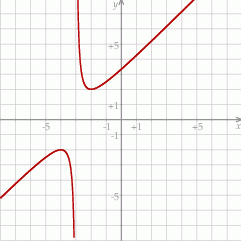
Dla ciekawskich, wykres funkcji 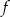 .
.