Zadanie nr 7208747
Wyznacz maksymalne przedziały monotoniczności funkcji 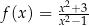 .
.
Rozwiązanie
Dziedziną danej funkcji jest zbiór
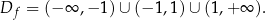
Pochodną obliczymy na dwa sposoby. W obu sposobach będziemy korzystać ze wzoru na pochodną ilorazu
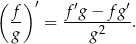
Sposób I
Zauważmy, że
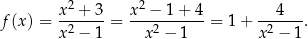
Mamy zatem
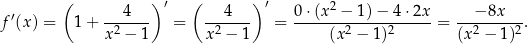
Widać teraz, że pochodna jest dodatnia dla 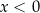 i ujemna dla
i ujemna dla 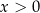 . Uwzględniając dziedzinę widzimy, że
. Uwzględniając dziedzinę widzimy, że 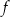 rośnie na przedziałach:
rośnie na przedziałach: 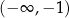 ,
, 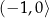 i maleje na przedziałach:
i maleje na przedziałach: 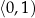 i
i 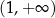 .
.
Sposób II
Liczymy pochodną
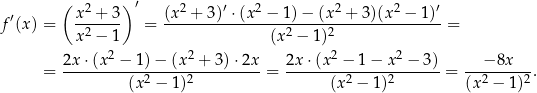
Monotoniczność wyznaczamy tak samo jak poprzednio.
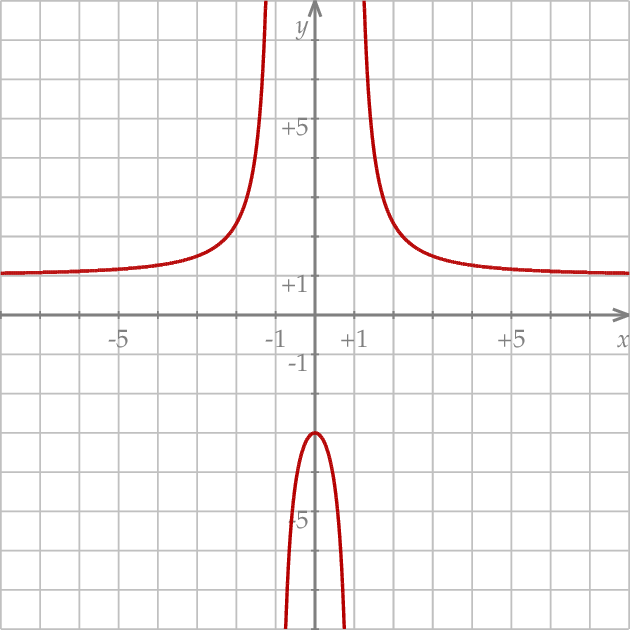
Na koniec dla ciekawskich wykres funkcji 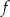 .
.
Odpowiedź: Rosnąca w 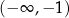 ,
, 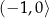 , malejąca w
, malejąca w 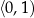 i
i 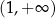 .
.

