Zadanie nr 4591081
Wyznacz przedziały monotoniczności funkcji 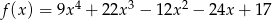 .
.
Rozwiązanie
Aby wyznaczyć przedziały monotoniczności liczymy pochodną.
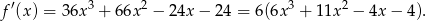
Szukamy teraz miejsc zerowych pochodnej – sprawdzamy najpierw dzielniki wyrazu wolnego, czyli liczby: 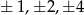 . Gdy to zrobimy okaże się, że jednym z pierwiastków pochodnej jest
. Gdy to zrobimy okaże się, że jednym z pierwiastków pochodnej jest 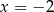 . Dzielimy teraz wielomian w nawiasie przez
. Dzielimy teraz wielomian w nawiasie przez 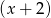 – można to zrobić na różne sposoby, my zrobimy to grupując wyrazy.
– można to zrobić na różne sposoby, my zrobimy to grupując wyrazy.
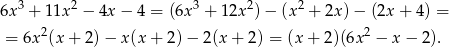
Rozkładamy teraz trójmian w nawiasie.
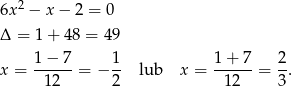
W takim razie
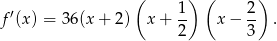
To oznacza, że pochodna jest dodatnia na przedziałach: 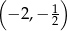 i
i 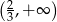 oraz ujemna na przedziałach
oraz ujemna na przedziałach 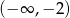 i
i 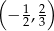 .
.

W takim razie funkcja 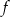 jest rosnąca na przedziałach
jest rosnąca na przedziałach 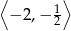 i
i 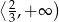 oraz malejąca na przedziałach
oraz malejąca na przedziałach 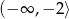 i
i 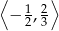 . Na koniec, dla ciekawskich, wykres funkcji
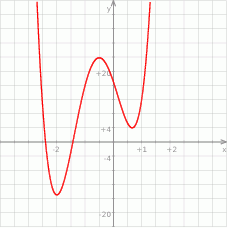
. Na koniec, dla ciekawskich, wykres funkcji 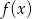 .
.
Odpowiedź: Rosnąca na 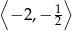 i
i 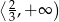 , malejąca na
, malejąca na 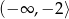 i
i 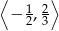 .
.

