Zadanie nr 4138624
Z przedziału ![[0,1]](https://img.zadania.info/zad/4138624/HzadT0x.gif) wybrano losowo dwa punkty, które podzieliły go na trzy odcinki. Jaka jest szansa, że uda się z nich zbudować trójkąt?
wybrano losowo dwa punkty, które podzieliły go na trzy odcinki. Jaka jest szansa, że uda się z nich zbudować trójkąt?
Rozwiązanie
Sposób I
O losowaniu dwóch punktów z przedziału ![[0,1]](https://img.zadania.info/zad/4138624/HzadR0x.gif) możemy myśleć jak o losowaniu jednego punktu
możemy myśleć jak o losowaniu jednego punktu 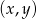 z kwadratu
z kwadratu ![[0 ,1]× [0,1]](https://img.zadania.info/zad/4138624/HzadR2x.gif) .
.
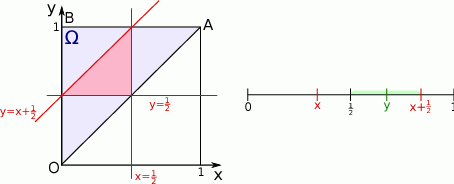
Wygodniej jest jednak trochę zmniejszyć przestrzeń zdarzeń elementarnych. Możemy założyć, że  oznacza mniejszą z wylosowanych liczb, czyli, że
oznacza mniejszą z wylosowanych liczb, czyli, że 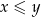 . W ten sposób obcinamy przestrzeń zdarzeń elementarnych do części kwadratu leżącej powyżej prostej
. W ten sposób obcinamy przestrzeń zdarzeń elementarnych do części kwadratu leżącej powyżej prostej 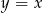 , czyli do trójkąta
, czyli do trójkąta 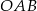 .
.
Teraz zastanówmy się kiedy z wylosowanych odcinków można zbudować trójkąt? Z trzech odcinków można zbudować trójkąt jeżeli najdłuższy z nich jest krótszy od sumy dwóch pozostałych. W naszej sytuacji oznacza to, że najdłuższy odcinek musi być krótszy od 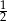 (bo suma długości wszystkich to 1).
(bo suma długości wszystkich to 1).
Wiemy już, co oznacza warunek z trójkątem, więc zastanówmy się jak mogą być położne punkty  i
i 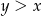 .
.
Jeżeli 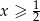 to odcinek
to odcinek ![[0,x]](https://img.zadania.info/zad/4138624/HzadR12x.gif) ma długość większą od
ma długość większą od 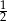 i jest źle. Zatem musi być
i jest źle. Zatem musi być 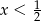 . Rysujemy więc prostą
. Rysujemy więc prostą 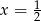 i pamiętamy, że zdarzenia sprzyjające muszą być na lewo od niej.
i pamiętamy, że zdarzenia sprzyjające muszą być na lewo od niej.
Teraz pora na 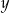 . Oczywiście
. Oczywiście 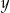 jest na prawo od
jest na prawo od  i podobnie jak przed chwilą, jeżeli
i podobnie jak przed chwilą, jeżeli 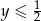 to odcinek
to odcinek ![[y,1 ]](https://img.zadania.info/zad/4138624/HzadR20x.gif) jest dłuższy od
jest dłuższy od 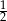 . Zatem
. Zatem 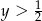 . Zaznaczamy to jak wcześniej: rysujemy prostą
. Zaznaczamy to jak wcześniej: rysujemy prostą 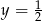 i pamiętamy, że zdarzenia sprzyjające są powyżej tej prostej.
i pamiętamy, że zdarzenia sprzyjające są powyżej tej prostej.
Ostatnia rzecz, na którą musimy uważać, to długość odcinka ![[x,y]](https://img.zadania.info/zad/4138624/HzadR24x.gif) . Musi ona być mniejsza niż
. Musi ona być mniejsza niż 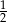 , czyli
, czyli
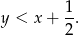
Jak poprzednio, rysujemy prostą 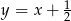 i zdarzenia sprzyjające są poniżej tej prostej.
i zdarzenia sprzyjające są poniżej tej prostej.
Ostatecznie widzimy, że zdarzenia sprzyjające tworzą trójkąt, którego pole stanowi 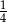 pola trójkąta
pola trójkąta 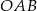 , czyli szukane prawdopodobieństwo wynosi
, czyli szukane prawdopodobieństwo wynosi 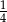 .
.
Sposób II
Mała modyfikacja poprzedniego sposobu.
Tak jak poprzednio stwierdzamy, że musimy policzyć miarę zbioru par 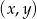 spełniających opisany w zadaniu warunek. Podobnie jak poprzednio przyjmijmy, że
spełniających opisany w zadaniu warunek. Podobnie jak poprzednio przyjmijmy, że 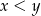 (czyli przez
(czyli przez  oznaczamy mniejszą z wylosowanych liczb). Tym razem nie będziemy jednak niczego rysować w układzie współrzędnych, ale szukane pole liczymy z twierdzenia Fubiniego (czyli zamiast całki podwójnej, liczymy całki iterowane).
oznaczamy mniejszą z wylosowanych liczb). Tym razem nie będziemy jednak niczego rysować w układzie współrzędnych, ale szukane pole liczymy z twierdzenia Fubiniego (czyli zamiast całki podwójnej, liczymy całki iterowane).
Ustalmy ![x ∈ [0,1]](https://img.zadania.info/zad/4138624/HzadR34x.gif) i zastanówmy się jaka jest miara możliwych
i zastanówmy się jaka jest miara możliwych ![y ∈ [0,1]](https://img.zadania.info/zad/4138624/HzadR35x.gif) . Dokładnie tak jak poprzednio stwierdzamy, że musi być
. Dokładnie tak jak poprzednio stwierdzamy, że musi być 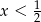 oraz
oraz 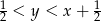 , zatem przy ustalonym
, zatem przy ustalonym  , możliwych
, możliwych 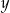 -ków jest
-ków jest  (długość przedziału
(długość przedziału ![[ 1 1] 2,x+ 2](https://img.zadania.info/zad/4138624/HzadR41x.gif) ). Zatem pole zbioru zdarzeń sprzyjających jest równe
). Zatem pole zbioru zdarzeń sprzyjających jest równe
![[ ]1 ∫ 12 1 2 2 1 xdx = --x = -. 0 2 0 8](https://img.zadania.info/zad/4138624/HzadR42x.gif)
Pole 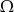 -i liczymy podobnie
-i liczymy podobnie
![∫ 1 [ ] 1 |Ω | = (1 − x )dx = x − 1x2 = 1- 0 2 0 2](https://img.zadania.info/zad/4138624/HzadR44x.gif)
(bo ![y ∈ [x ,1]](https://img.zadania.info/zad/4138624/HzadR45x.gif) ). Zatem prawdopodobieństwo jest równe
). Zatem prawdopodobieństwo jest równe
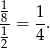
Sposób III
Zamiast myśleć o losowaniu dwóch liczb z odcinka, możemy myśleć o losowaniu trzech liczb z okręgu długości 1– dodatkowy punkt to ten, w którym rozcinamy okrąg, żeby dostać odcinek. Łatwo teraz zauważyć, że zdarzenia sprzyjające to takie, w których te trzy punkty nie leżą na jednym półokręgu.
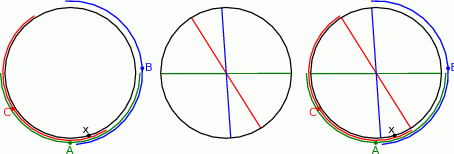
Zauważmy teraz, że punkt na okręgu jednoznacznie wyznacza półokrąg, którego jest środkiem. Kolejna obserwacja to, że trzy punkty leżą na jednym półokręgu wtedy i tylko wtedy, gdy wyznaczone przez te punkty półokręgi mają niepustą część wspólną. Spróbujmy to uzasadnić: jeżeli punkty leżą na jednym półokręgu, to środek tego półokręgu jest w każdym z półokręgów wyznaczonych przez te trzy punkty. Na odwrót, jeżeli  jest punktem wspólnym trzech półokręgów wyznaczonych przez dane punkty, to punkty te leżą na półokręgu o środku
jest punktem wspólnym trzech półokręgów wyznaczonych przez dane punkty, to punkty te leżą na półokręgu o środku  .
.
Powyższe obserwacje pozwalają nam sprafrazować zadanie: losujemy trzy półokręgi, jakie jest prawdopodobieństwo 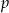 , że ich część wspólna jest pusta?
, że ich część wspólna jest pusta?
Łatwiej jest policzyć prawdopodobieństwo 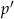 zdarzenia przeciwnego: jakie jest prawdopodobieństwo wylosowania trzech półokręgów, które mają niepustą część wspólną? Półokręgi możemy losować następująco: losujemy trzy średnice, a potem dla każdej ze średnic wybieramy jeden z wyznaczonych przez nie półokręgów. Pokażemy, że w tym drugim etapie, czyli przy wyborze półokręgów, interesujące nas prawdopodobieństwo otrzymania przecinających się łuków wynosi
zdarzenia przeciwnego: jakie jest prawdopodobieństwo wylosowania trzech półokręgów, które mają niepustą część wspólną? Półokręgi możemy losować następująco: losujemy trzy średnice, a potem dla każdej ze średnic wybieramy jeden z wyznaczonych przez nie półokręgów. Pokażemy, że w tym drugim etapie, czyli przy wyborze półokręgów, interesujące nas prawdopodobieństwo otrzymania przecinających się łuków wynosi  (jest więc niezależne od tego jakie średnice wylosowano). To oznacza, że
(jest więc niezależne od tego jakie średnice wylosowano). To oznacza, że 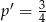 , czyli
, czyli 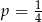 .
.
Ustalmy zatem trzy średnice i zastanówmy się jakie jest prawdopodobieństwo wybrania trzech półokręgów, które mają niepusty przekrój. Zauważmy, że mamy już teraz sytuację skończoną, czyli prawdopodobieństwo klasyczne! Każda średnica wyznacza dwa półokręgi, czyli
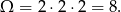
Zdarzeń sprzyjających jest tyle, na ile łuków dzielą okrąg trzy średnice, czyli 6. Rzeczywiście, jeżeli półokręgi mają mieć część wspólną, to musi to być jeden z tych 6 łuków. Odwrotnie też, łatwo zobaczyć, że każdy z tych łuków jednoznacznie wyznacza trzy półokręgi. Zatem prawdopodobieństwo wybrania trzech przecinających się półokręgów wynosi
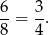
W pierwszej chwili może się wydawać, że 3 sposób jest przesadnie skomplikowany w stosunku do dwóch poprzednich, ale ma on jedną dużą zaletę, można go z powodzeniem stosować w ogólniejszych sytuacjach (np. gdy na okręgu wybieramy nie 3, ale  punktów).
punktów).
Odpowiedź: