/Studia/Prawdopodobieństwo/Wariancja

Zadanie nr 4472581

Dodaj do ulubionych
Dodaj do rozwiązanych

W jednej urnie są 3 kulki białe i 5 kulek czarnych. W drugiej urnie znajdują się 2 kulki czerwone i 3 kulki niebieskie. Doświadczenie polega na jednoczesnym losowaniu po jednej kulce z obu urn.

  • Opisz przestrzeń zdarzeń elementarnych 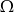Ω i oblicz ile elementów ma ten zbiór.
  • Umawiamy się, ze za wylosowanie kulki białej otrzymuje się 16 złotych, kulki czerwonej 16 złotych, kulki czarnej 17 złotych i kulki niebieskiej 17 złotych. Wyznacz zmienną losowa określoną na przez powyższe zasady.
  • Oblicz wartość oczekiwaną powyższej zmiennej losowej.
  • Oblicz wariancję i odchylenie standardowe powyższej zmiennej.

Rozwiązanie

  • Za zdarzenia elementarne możemy przyjąć pary wylosowanych kul. Mamy więc
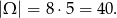
    |Ω | = 8⋅ 5 = 40.

     
    Odpowiedź: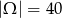 |Ω | = 40

  • Opisana zmienna losowa przyjmuje 4 wartości: 16+16=32 zł jeżeli z pierwszej urny wylosowaliśmy kulkę białą, a z drugiej kulkę czerwoną. Od razu zauważmy, że zdarzenie takie zachodzi z prawdopodobieństwem
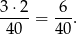
    3-⋅2 6-- 40 = 40.

    Zmienna przyjmie wartość 17+17=34 zł jeżeli z pierwszej wylosujemy kulkę czarną, a z drugiej kulkę niebieską. Taka sytuacja zachodzi a prawdopodobieństwem

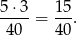
    5 ⋅3 15 ---- = --. 40 40

    W pozostałych przypadkach wartość zmiennej losowej wynosi 16+17=33 zł. Ta sytuacja zdarza się z prawdopodobieństwem

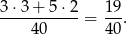
    3-⋅3+--5⋅2-= 19-. 40 40
  • Liczymy
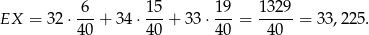
    6 15 19 1329 EX = 32⋅ ---+ 34 ⋅---+ 33⋅ ---= -----= 33,225. 40 40 40 40

     
    Odpowiedź: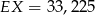 EX = 33,225

  • Liczymy wariancję
    2 2 D X = E[(X − EX ) ] = 2 6 2 15 2 19 = (− 1,225) ⋅---+ (0 ,775) ⋅ ---+ (− 0,225) ⋅---= 40 40 40 = 18-,9-75 = 0,4 74375. 4 0

    Teraz odchylenie standardowe

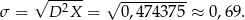
    √ --2-- √ --------- σ = D X = 0,47 4375 ≈ 0 ,6 9.

     
    Odpowiedź: D 2X = 0,47437 5, σ = 0,69

Wersja PDF