/Studia/Prawdopodobieństwo/Wariancja

Zadanie nr 9259416

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucono 4 razy symetryczną monetą. Oblicz wariancję liczby wyrzuconych orłów. Podaj wynik z dokładnością do 0,001.

Rozwiązanie

Przy czterech rzutach monetą mamy 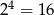4 2 = 16 możliwych wyników (uzwględniamy kolejność), pogrupujmy je w zależności od liczby otrzymanych orłów.
0 orłów: (R,R,R,R) 1 wynik
1 orzeł: (O,R,R,R), (R,O,R,R), (R,R,O,R), (R,R,R,O) 4 wyniki
2 orły: (O,O,R,R), (O,R,O,R), (R,O,O,R), (O,R,R,O), (R,O,R,O), (R,R,O,O) 6 wyników
3 orły: (O,O,O,R), (O,O,R,O), (O,R,O,O), (R,O,O,O) 4 wyniki
4 orły: (O,O,O,O) 1 wynik
Oczywiście, mogliśmy to samo wyliczyć używając schematu Bernoullego.

Liczymy teraz wartość oczekiwaną liczby orłów

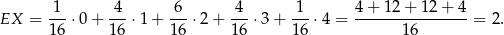
1 4 6 4 1 4 + 12 + 12 + 4 EX = ---⋅0 + ---⋅ 1+ ---⋅2+ ---⋅3 + ---⋅4 = ----------------= 2. 16 1 6 16 16 1 6 16

Wynik ten nie powinien dziwić, zmienne losowe ’ilość orłów’ i ’ilość reszek’ mają takie same rozkłady, ich suma jest równa 4, więc z addytywności wartości oczekiwanej, wartość oczekiwana każdej z nich jest równa 2.

Liczymy teraz wariancję.

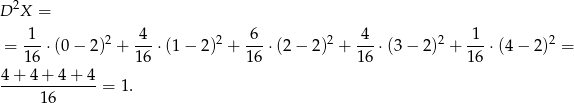
2 D X = 1 2 4 2 6 2 4 2 1 2 = ---⋅(0 − 2) + ---⋅(1 − 2 ) + --⋅ (2− 2) + ---⋅(3− 2) + ---⋅(4− 2) = 16 1 6 16 16 16 4-+-4-+-4-+-4 = 1 . 1 6

 
Odpowiedź: 1

Wersja PDF