/Szkoła średnia/Prawdopodobieństwo/Z definicji/Karty

Zadanie nr 4685783

Dodaj do ulubionych
Dodaj do rozwiązanych

Z talii 52 kart losujemy jedną kartę.

  • Oblicz prawdopodobieństwo zdarzeń:
    A – losowo wybrana karta jest pikiem.
    B – losowo wybrana karta jest asem.
  • Oblicz prawdopodobieństwo zdarzeń 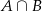A ∩ B oraz A ∪ B .

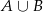Rozwiązanie

  • W talii są cztery kolory: piki, trefle, kiery i kara. Zatem w talii mamy
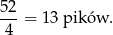
    52-= 13 pików. 4

    Zatem

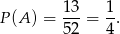
    13 1 P (A ) = ---= -. 52 4

    W talii są cztery asy, więc

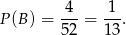
    4 1 P(B ) = 52-= 13-.

     
    Odpowiedź: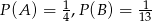 P (A ) = 14,P (B) = 113

  • Zauważmy, że zdarzenie 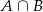A ∩ B oznacza wylosowanie asa pik, czyli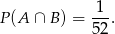
    1 P(A ∩ B ) = ---. 5 2

    Zdarzenie 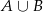A ∪ B obliczymy ze wzoru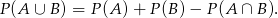

    P (A ∪ B ) = P(A ) + P (B)− P(A ∩ B).

    Liczymy

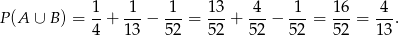
    P (A ∪ B ) = 1-+ -1-− 1--= 13-+ -4-− 1--= 16-= 4-. 4 1 3 52 52 5 2 52 52 13

     
    Odpowiedź: 1- -4 P(A ∩ B) = 52,P(A ∪ B ) = 13

Wersja PDF