Zdarzenia losowe 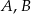 są zawarte w
są zawarte w 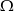 oraz
oraz 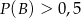 . Wykaż, że
. Wykaż, że
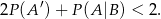
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Zdarzenia losowe 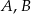 są zawarte w
są zawarte w 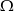 oraz
oraz 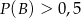 . Wykaż, że
. Wykaż, że
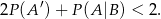
Zdarzenia losowe 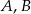 są zawarte w
są zawarte w 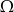 oraz
oraz 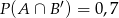 (
(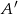 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 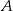 ,
, 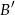 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 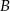 ). Wykaż, że
). Wykaż, że 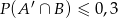 .
.
O zdarzeniach losowych 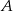 i
i 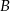 wiemy, że:
wiemy, że: 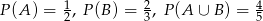 . Oblicz:
. Oblicz:
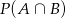
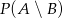
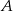 i
i 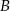 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 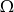 , że
, że 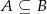 oraz
oraz 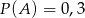 i
i 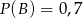 . Oblicz prawdopodobieństwo różnicy
. Oblicz prawdopodobieństwo różnicy 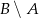 .
.
Prawdopodobieństwa zdarzeń 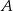 i
i 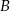 oraz zdarzeń do nich przeciwnych spełniają warunki:
oraz zdarzeń do nich przeciwnych spełniają warunki: 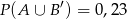 i
i 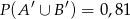 .
.
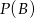 .
. 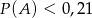 to
to 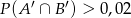 .
.O zdarzeniach losowych 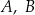 wiadomo, że:
wiadomo, że: 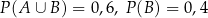 i
i 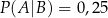 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 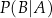 .
.
O zdarzeniach losowych 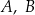 wiadomo, że:
wiadomo, że: 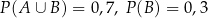 i
i 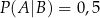 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 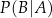 .
.
Znając prawdopodobieństwa zdarzeń 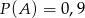 ,
, 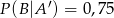 ,
, 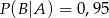 , gdzie
, gdzie 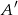 oznacza zdarzenie przeciwne do
oznacza zdarzenie przeciwne do 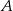 , oblicz prawdopodobieństwo zdarzenia
, oblicz prawdopodobieństwo zdarzenia 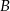 .
.
Wiadomo, że zdarzenia 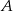 i
i 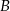 są niezależne oraz
są niezależne oraz 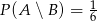 ,
, 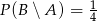 . Oblicz
. Oblicz 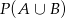 .
.
Uzasadnij, że
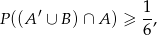
jeżeli 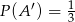 i
i 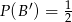 .
.
Wiedząc, że 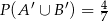 oraz
oraz 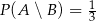 . Wykaż, że
. Wykaż, że 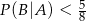 .
.
Dane są dwa takie zdarzenia 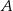 i
i 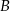 , że
, że 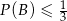 i
i 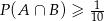 . Czy może zachodzić równość
. Czy może zachodzić równość 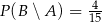 ? Odpowiedź uzasadnij.
? Odpowiedź uzasadnij.
Dla zdarzeń 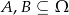 spełnione są warunki
spełnione są warunki 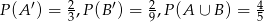 . Oblicz
. Oblicz 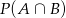 .
.
Zdarzenia 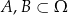 spełniają warunki
spełniają warunki 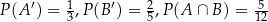 . Wyznacz
. Wyznacz 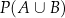 .
.
O zdarzeniach 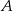 i
i 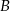 wiadomo, że
wiadomo, że 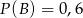 ,
, 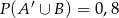 ,
, 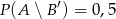 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 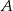 .
.
Wiadomo, że 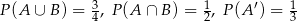 . Oblicz prawdopodobieństwa zdarzeń
. Oblicz prawdopodobieństwa zdarzeń 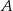 i
i 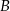 .
.
O zdarzeniach losowych 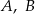 wiadomo, że:
wiadomo, że: 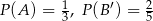 i
i 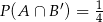 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 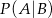 .
.
Niech 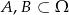 będą zdarzeniami losowymi, takimi że
będą zdarzeniami losowymi, takimi że 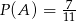 i
i 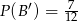 . Uzasadnij, że
. Uzasadnij, że 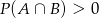 .
.
Wiedząc, że 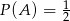 ,
, 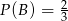 ,
, 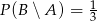 , oblicz
, oblicz 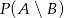 .
.
Dane są zdarzenia losowe 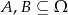 takie, że
takie, że 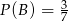 i
i 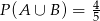 . Oblicz
. Oblicz 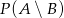 , gdzie zdarzenie
, gdzie zdarzenie 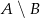 oznacza różnicę zdarzeń
oznacza różnicę zdarzeń 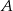 i
i 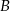 .
.
Dane są zdarzenia losowe 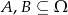 takie, że
takie, że 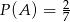 i
i 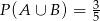 . Oblicz
. Oblicz 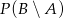 , gdzie zdarzenie
, gdzie zdarzenie 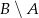 oznacza różnicę zdarzeń
oznacza różnicę zdarzeń 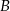 i
i 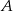 .
.
O zdarzeniach losowych 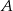 i
i 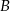 wiadomo, że
wiadomo, że 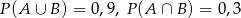 i
i 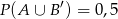 . Oblicz
. Oblicz 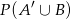 .
.
Niech 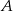 ,
, 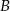 będą zdarzeniami o prawdopodobieństwach
będą zdarzeniami o prawdopodobieństwach 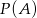 i
i 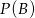 . Wykaż, że jeżeli
. Wykaż, że jeżeli 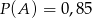 i
i 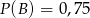 , to prawdopodobieństwo warunkowe spełnia nierówność
, to prawdopodobieństwo warunkowe spełnia nierówność 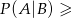 0,8.
0,8.
Zdarzenia losowe 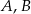 są zawarte w
są zawarte w 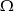 oraz
oraz 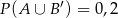 . Wykaż, że
. Wykaż, że 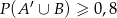 .
.
