W trójkącie 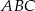 prowadzimy dwusieczną kąta
prowadzimy dwusieczną kąta  i przez punkt
i przez punkt 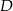 przecięcia się tej dwusiecznej z bokiem
przecięcia się tej dwusiecznej z bokiem 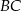 prowadzimy proste równoległe do boków
prowadzimy proste równoległe do boków 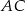 i
i 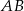 , które przecinają te boki odpowiednio w punktach
, które przecinają te boki odpowiednio w punktach 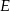 i
i 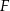 . Wykaż, że czworokąt
. Wykaż, że czworokąt 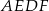 jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
/Szkoła podstawowa/Geometria/Trójkąt/Dowolny
Na rysunku przedstawiono trójkąt 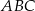 , w którym
, w którym 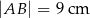 oraz odcinek
oraz odcinek 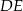 równoległy do boku
równoległy do boku 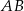 trójkąta, którego długość jest równa 6 cm.
trójkąta, którego długość jest równa 6 cm.
Pole trójkąta  jest równe
jest równe 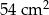 , a pole trapezu
, a pole trapezu 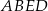 jest o 25% większe od pola trójkąta
jest o 25% większe od pola trójkąta 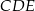 . Oblicz wysokość trapezu
. Oblicz wysokość trapezu 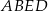 .
.
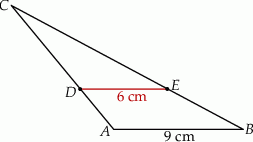
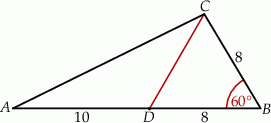
Oblicz pole trójkąta, którego wymiary podano na rysunku.
Punkt 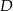 jest środkiem boku
jest środkiem boku 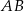 trójkąta
trójkąta 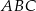 , w którym
, w którym 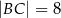 ,
, 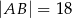 i
i 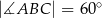 . Oblicz pole trójkąta
. Oblicz pole trójkąta 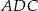 .
.
W trójkącie 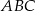 , w którym
, w którym 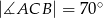 połączono środek okręgu wpisanego
połączono środek okręgu wpisanego 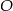 z wierzchołkami
z wierzchołkami 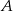 i
i 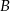 . Oblicz miarę kąta
. Oblicz miarę kąta 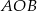 .
.
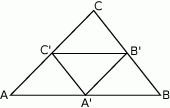
Punkty  są środkami boków trójkąta
są środkami boków trójkąta  . Pole trójkąta
. Pole trójkąta 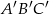 jest równe 4. Oblicz pole trójkąta
jest równe 4. Oblicz pole trójkąta  .
.
Uzasadnij, że oba kąty przy podstawie  trójkąta
trójkąta  są równe.
są równe.
Środkowa  trójkąta
trójkąta  ma długość równą połowie długości boku
ma długość równą połowie długości boku 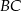 . Miara kąta między tą środkową a wysokością
. Miara kąta między tą środkową a wysokością 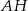 jest równa
jest równa 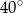 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 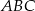 .
.
Dwa spośród boków trójkąta mają długości 3 i 5. Zaznacz na osi liczbowej wszystkie liczby oznaczające możliwe długości trzeciego boku.
Dany jest trójkąt 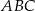 . Punkt
. Punkt 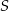 jest środkiem boku
jest środkiem boku 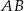 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 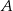 i
i 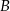 od prostej
od prostej 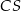 są równe.
są równe.
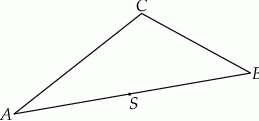
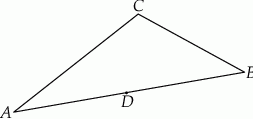
Na boku 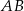 trójkąta
trójkąta 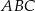 wybrano punkt
wybrano punkt  w ten sposób, że odległości punktów
w ten sposób, że odległości punktów  i
i  od prostej
od prostej 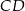 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 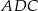 i
i 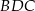 mają równe pola.
mają równe pola.
Na środkowej 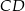 trójkąta
trójkąta 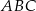 wybrano punkt
wybrano punkt 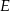 . Wykaż, że trójkąty
. Wykaż, że trójkąty  i
i 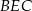 mają równe pola.
mają równe pola.
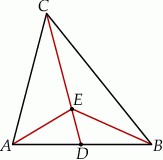
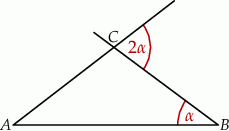
Oblicz miarę kąta  .
.
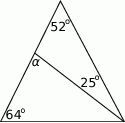
Oblicz miarę kąta  .
.
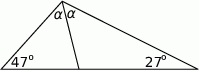
Oblicz miarę kąta  .
.
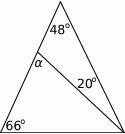
Oblicz miarę kąta  .
.
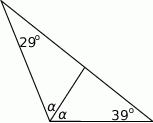
Oblicz miarę kąta  .
.
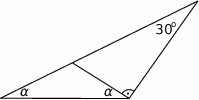
Oblicz miarę kąta  .
.
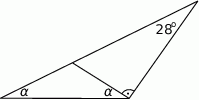
Oblicz miarę kąta  .
.
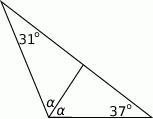
Oblicz miarę kąta  .
.
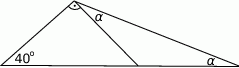
Oblicz miarę kąta  .
.
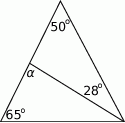
Prosta 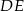 jest równoległa do boku
jest równoległa do boku 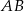 trójkąta
trójkąta 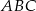 i przecina bok
i przecina bok 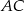 w punkcie
w punkcie 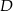 , bok
, bok 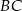 w punkcie
w punkcie 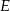 . Oblicz
. Oblicz 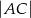 jeśli
jeśli 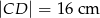 ,
, 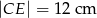 i
i 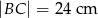 .
.
Prosta 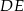 jest równoległa do boku
jest równoległa do boku 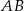 trójkąta
trójkąta 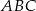 i przecina bok
i przecina bok 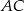 w punkcie
w punkcie  , bok
, bok 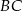 w punkcie
w punkcie 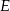 . Oblicz
. Oblicz 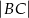 , jeśli
, jeśli 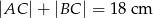 ,
, 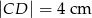 i
i 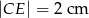 .
.
Prosta 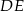 jest równoległa do boku
jest równoległa do boku 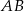 trójkąta
trójkąta 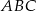 i przecina bok
i przecina bok 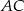 w punkcie
w punkcie 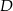 , bok
, bok 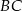 w punkcie
w punkcie 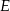 . Oblicz
. Oblicz 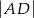 jeśli
jeśli 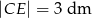 ,
, 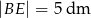 i
i 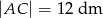 .
.
Wierzchołek 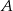 trójkąta ostrokątnego
trójkąta ostrokątnego 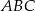 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 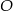 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 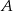 poprowadzono wysokość
poprowadzono wysokość 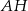 . Wykaż, że
. Wykaż, że 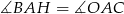 .
.
Trójkąt o bokach 6, 8 i 10 jest podobny do trójkąta o obwodzie 216. Oblicz długości boków drugiego trójkąta.
Trójkąt o bokach 12, 9 i 15 jest podobny do trójkąta o obwodzie 108. Oblicz długości boków drugiego trójkąta.
W trójkącie 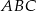 przedłużono bok
przedłużono bok 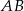 poza wierzchołek
poza wierzchołek 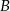 i odłożono odcinek
i odłożono odcinek 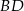 taki, że
taki, że 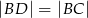 . Następnie połączono punkty
. Następnie połączono punkty 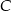 i
i 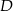 (rysunek). Wykaż, że
(rysunek). Wykaż, że 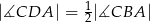 .
.
W trójkącie 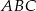 przedłużono bok
przedłużono bok 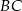 poza wierzchołek
poza wierzchołek 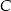 i odłożono odcinek
i odłożono odcinek 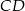 taki, że
taki, że 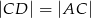 . Następnie połączono punkty
. Następnie połączono punkty 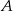 i
i 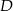 (rysunek). Wykaż, że
(rysunek). Wykaż, że 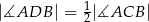 .
.
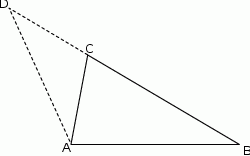
Na dwusiecznej 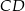 trójkąta
trójkąta 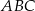 , w którym
, w którym 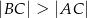 wybrano punkt
wybrano punkt 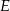 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 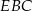 jest większe od pola trójkąta
jest większe od pola trójkąta 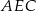 .
.
W trójkącie 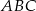 dane są:
dane są: 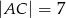 ,
, 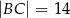 i
i 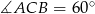 . Oblicz pole trójkąta
. Oblicz pole trójkąta 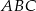 .
.
Dwusieczne kątów przyległych do boku 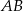 trójkąta
trójkąta 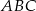 przecinają się w punkcie
przecinają się w punkcie 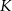 . Odległość punktu
. Odległość punktu 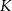 od odcinka
od odcinka 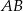 wynosi 3. Jaka jest odległość punktu
wynosi 3. Jaka jest odległość punktu 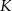 od odcinka
od odcinka 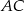 ?
?
Symetralna boku 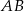 trójkąta
trójkąta 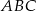 przecina bok
przecina bok 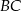 w punkcie
w punkcie 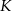 , przy czym odcinek
, przy czym odcinek 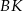 ma długość 5. Jaką długość ma odcinek
ma długość 5. Jaką długość ma odcinek 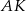 ?
?
Ile jest trójkątów o obwodzie równym 19, w których długości boków wyrażone są liczbami całkowitymi. Wymień je.

