/Szkoła podstawowa/Geometria/Trójkąt/Dowolny

Zadanie nr 7613109

Dodaj do ulubionych
Dodaj do rozwiązanych

Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 12. Wyznacz obwód każdego z tych trójkątów.

Rozwiązanie

Oznaczmy przez 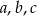a,b,c długości boków jednego trójkąta i przez 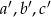′ ′ ′ a ,b,c długości boków drugiego oraz przez 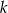k skalę podobieństwa trójkątów. Stosunek pól figur podobnych jest kwadratem skali podobieństwa. Zatem

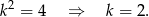
k2 = 4 ⇒ k = 2 .

Stosunek obwodów figur podobnych jest równy skali podobieństwa, więc

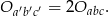
Oa′b′c′ = 2Oabc .

Zatem

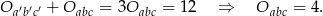
O ′ ′′ + O = 3O = 1 2 ⇒ O = 4. abc abc abc abc

Stąd

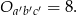
O ′ ′′ = 8. a bc

 
Odpowiedź: 4 i 8

Wersja PDF