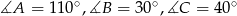Zadanie nr 8659883
Wysokość 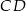 trójkąta
trójkąta 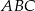 tworzy z bokami
tworzy z bokami 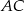 i
i 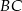 kąty o miarach równych odpowiednio
kąty o miarach równych odpowiednio 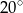 i
i 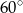 . Punkt
. Punkt 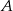 należy do odcinka
należy do odcinka 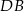 .
.
- Narysuj trójkąt
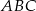 i jego wysokość
i jego wysokość 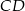 .
. - Wyznacz miary kątów trójkąta
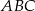 .
.
Rozwiązanie
- Z podanej informacji o tym, że punkt
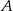 jest na odcinku
jest na odcinku 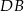 wynika, że punkt
wynika, że punkt 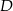 jest na zewnątrz odcinka
jest na zewnątrz odcinka 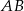 i na lewo od punktu
i na lewo od punktu 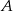 . Oznacza to, że trójkąt
. Oznacza to, że trójkąt 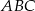 jest rozwartokątny.
jest rozwartokątny. 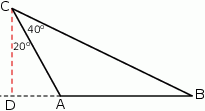
- Znamy dwa kąty trójkąta
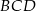 , możemy więc wyliczyc jego trzeci kąt.
, możemy więc wyliczyc jego trzeci kąt. 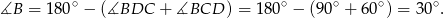
Pozostało policzyć kąt przy wierzchołku
 .
. 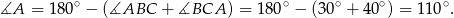
Odpowiedź: