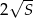/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Najmniejsza długość

Zadanie nr 4429530

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz jaka może być najmniejsza możliwa długość przeciwprostokątnej trójkąta prostokątnego o polu 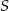S .

Rozwiązanie

Szkicujemy trójkąt prostokątny.

PIC

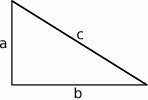
Sposób I

Wiemy, że 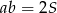ab = 2S , a próbujemy ustalić jaka jest najmniejsza możliwa wartość wyrażenia

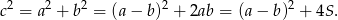
c2 = a2 + b2 = (a − b)2 + 2ab = (a − b)2 + 4S .

Widać teraz, że najmniejszą możliwą długość przeciwprostokątnej otrzymamy, gdy 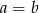a = b . Wtedy

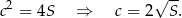
2 √ -- c = 4S ⇒ c = 2 S.

Sposób II

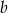Liczby a i b są rozwiązaniami układu równań

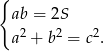
{ ab = 2S 2 2 2 a + b = c .

Podstawiamy 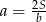2S a = b z pierwszego równania do drugiego i mamy

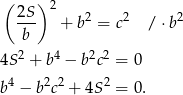
( 2S) 2 --- + b2 = c2 / ⋅b 2 b 4S 2 + b4 − b 2c2 = 0 b 4 − b2c2 + 4S 2 = 0.

Jest to równanie dwukwadratowe, więc podstawiamy 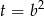t = b2 .

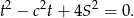
t2 − c2t + 4S2 = 0 .

Równanie to musi mieć rozwiązania, więc musi być spełniony warunek

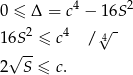
0 ≤ Δ = c4 − 16S2 2 4 √4- 16√S--≤ c / 2 S ≤ c.

Z drugiej strony widać, że taką wartość długości przeciwprostokątnej możemy otrzymać, gdy 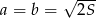√ --- a = b = 2S .

Sposób III

Tak jak w poprzednim sposobie ustalamy, że

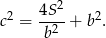
4S 2 c2 = ----+ b2. b2

Pozostało teraz wyznaczyć najmniejszą wartość funkcji

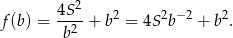
4S2 f(b) = ----+ b2 = 4S2b−2 + b2. b2

Liczymy pochodną.

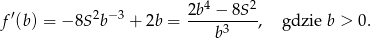
2b4 − 8S 2 f′(b) = − 8S2b− 3 + 2b = ----------, gdzie b > 0. b3

Licznik otrzymanego wyrażenia zeruje się dla 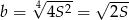√4---2 √ --- b = 4S = 2S , a na lewo od tego punktu pochodna jest ujemna (czyli funkcja 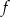f maleje), na prawo pochodna jest dodatnia (funkcja jest rosnąca). Zatem dla tej wartości 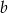b otrzymamy najmniejszą możliwą wartość funkcji f .

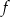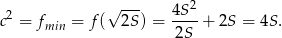
2 √ --- 4S 2 c = fmin = f( 2S ) = -2S-+ 2S = 4S .

Zatem najmniejsza możliwa długość przeciwprostokątnej to 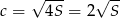√ --- √ -- c = 4S = 2 S .  
Odpowiedź: √ -- 2 S

Wersja PDF