/Konkursy/Zadania/Równania/Wielomianowe/Stopnia 3

Zadanie nr 5962866

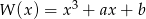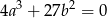Wykaż, że jeżeli wielomian 3 W (x) = x + ax + b ma pierwiastek dwukrotny, to 4a3 + 27b 2 = 0 .

Wersja PDF

Rozwiązanie

Sposób I

Zadanie najprościej jest rozwiązać przy pomocy pochodnej. Łatwo uzasadnić, że jeżeli 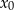x0 jest pierwiastkiem wielokrotnym wielomianu to jest też pierwiastkiem jego pochodnej. W naszej sytuacji mamy

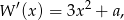
W ′(x ) = 3x2 + a,

daje układ równań

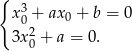
{ x3+ ax0 + b = 0 02 3x0 + a = 0.

Zapiszmy pierwsze równanie w postaci 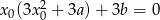x 0(3x20 + 3a)+ 3b = 0 i podstawmy za 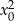x2 0 z drugiego równania

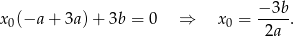
−-3b- x0(−a + 3a)+ 3b = 0 ⇒ x0 = 2a .

Podstawiamy to do drugiego równania.

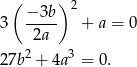
( ) 2 3 −-3b- + a = 0 2a 27b2 + 4a3 = 0.

Sposób II

Jeżeli wielomian ma mieć pierwiastek podwójny to musi być postaci 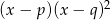(x− p)(x − q)2 . Zatem

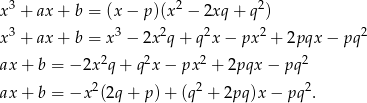
x3 + ax + b = (x − p )(x2 − 2xq + q2) x3 + ax + b = x 3 − 2x 2q+ q2x− px2 + 2pqx − pq2 2 2 2 2 ax + b = − 2x q+ q x− px + 2pqx − pq ax + b = −x 2(2q + p )+ (q2 + 2pq )x − pq2.

Równość ta oznacza, że 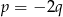p = − 2q oraz

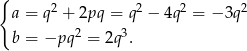
{ a = q2 + 2pq = q2 − 4q 2 = − 3q2 b = −pq 2 = 2q 3.

Teraz liczymy

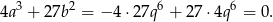
4a 3 + 27b 2 = − 4⋅2 7q6 + 27⋅ 4q6 = 0.

Dla ciekawskich, wyrażenie

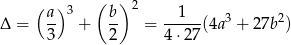
( )3 ( ) 2 Δ = a- + b- = --1---(4a3 + 27b2) 3 2 4 ⋅27

nazywa się wyróżnikiem wielomianu 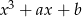x3 + ax+ b i podobnie jak dla trójmianu kwadratowego decyduje o ilości jego rozwiązań. Jeżeli 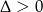Δ > 0 to równanie ma dokładnie jeden pierwiastek rzeczywisty. Jeżeli 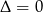Δ = 0 to dla 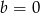b = 0 równanie ma jeden potrójny pierwiastek 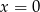x = 0 , a dla 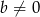b ⁄= 0 równanie ma dwa pierwiastki rzeczywiste i jeden z nich jest podwójny. Jeżeli natomiast 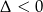Δ < 0 to równanie ma 3 różne pierwiastki rzeczywiste. Ponadto jest dość proste podstawienie sprowadzające dowolne równanie stopnia 3 do równania postaci 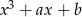3 x + ax+ b , więc w tym sensie powyższy komentarz dotyczy wszystkich równań stopnia 3. Jeżeli komuś mało, to niech przeczyta poradnik o wzorach Cardano.

Wersja PDF