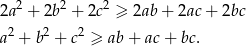Zadanie nr 8315206
Udowodnij, że dla dowolnych liczb 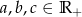 zachodzi nierówność
zachodzi nierówność
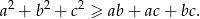
Rozwiązanie
Nierówność z treści zadania łatwo wynika z nierówności
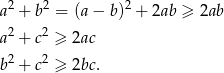
Dodając te nierówności stronami mamy
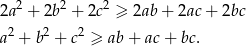
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Udowodnij, że dla dowolnych liczb 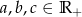 zachodzi nierówność
zachodzi nierówność
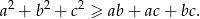
Nierówność z treści zadania łatwo wynika z nierówności
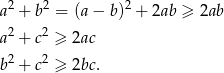
Dodając te nierówności stronami mamy