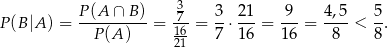Zadanie nr 3533455
Wiedząc, że 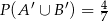 oraz
oraz 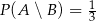 . Wykaż, że
. Wykaż, że 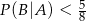 .
.
Rozwiązanie
Naszkicujmy diagram Venna.
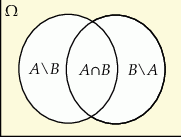
Z diagramu powinno być jasne, że
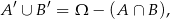
więc
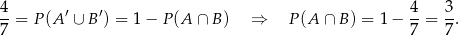
Stąd
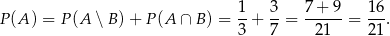
Mamy zatem
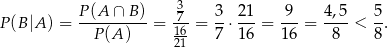
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiedząc, że 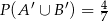 oraz
oraz 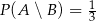 . Wykaż, że
. Wykaż, że 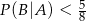 .
.
Naszkicujmy diagram Venna.

Z diagramu powinno być jasne, że
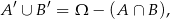
więc
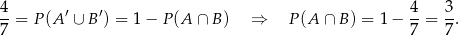
Stąd
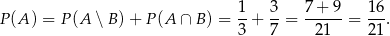
Mamy zatem