Zadanie nr 8444752
O zdarzeniach losowych 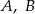 wiadomo, że:
wiadomo, że: 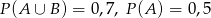 i
i 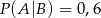 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 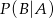 .
.
Rozwiązanie
Ponieważ 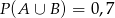 i
i 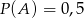 , to
, to
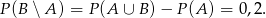
Wiemy ponadto, że
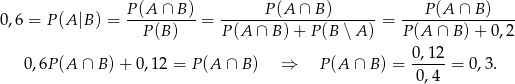
Stąd
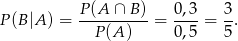
Odpowiedź: 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
O zdarzeniach losowych 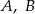 wiadomo, że:
wiadomo, że: 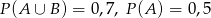 i
i 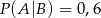 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 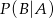 .
.
Ponieważ 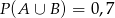 i
i 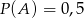 , to
, to
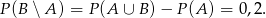
Wiemy ponadto, że
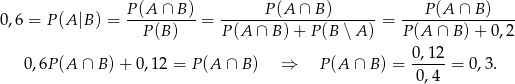
Stąd
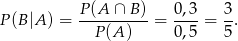
Odpowiedź: 
