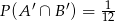/Szkoła średnia/Prawdopodobieństwo/Bez treści/Działania na zbiorach

Zadanie nr 7385600

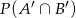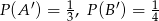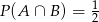Oblicz prawdopodobieństwo ′ ′ P (A ∩ B ) , jeśli ′ 1 ′ 1 P(A ) = 3, P(B ) = 4 i P (A ∩ B ) = 12 .

Wersja PDF

Rozwiązanie

Sposób I

Od razu mamy

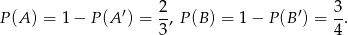
2 3 P (A) = 1− P(A ′) = -, P(B ) = 1− P(B ′) = -. 3 4
PIC

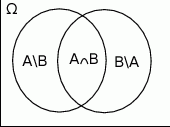
Jeżeli narysujemy sobie diagram Venna, to powinno być widać, że

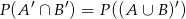
′ ′ ′ P (A ∩ B ) = P((A ∪ B) )

Jest to jedno z praw de’Morgana, można je czytać tak: w 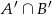′ ′ A ∩ B są zdarzenia, które nie są 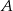A i nie są w 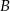B , czyli takie, które nie są 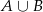A ∪ B . Pozostało teraz skorzystać ze znanego wzoru

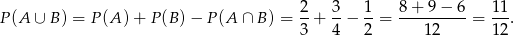
2 3 1 8 + 9 − 6 11 P(A ∪ B) = P (A )+ P (B) − P (A ∩ B) = --+ --− --= ----------= ---. 3 4 2 12 12

Zatem

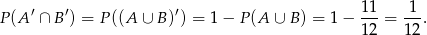
P(A ′ ∩ B ′) = P ((A ∪ B )′) = 1− P(A ∪ B ) = 1 − 11-= -1-. 12 12

Sposób II

Zamiast robić zadanie schematycznie, możemy od razu uważniej przyjrzeć się diagramowi Venna i zobaczyć, że

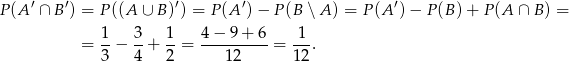
′ ′ ′ ′ ′ P(A ∩ B ) = P((A ∪ B )) = P(A )− P (B ∖A ) = P (A ) − P (B) + P(A ∩ B) = 1 3 1 4 − 9 + 6 1 = --− --+ --= ----------= ---. 3 4 2 12 12

 
Odpowiedź: P (A′ ∩ B′) = -1 12

Wersja PDF