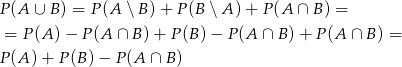Zadanie nr 7534735
Wykaż, że jeśli 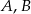 są dowolnymi zdarzeniami przestrzeni
są dowolnymi zdarzeniami przestrzeni 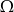 , to
, to 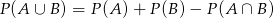 .
.
Rozwiązanie
Jeżeli narysujemy sobie diagram Venna, to widać, że
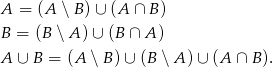
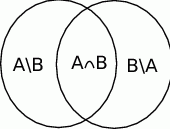
W wszystkich równościach zbiory po prawej stronie są rozłączne, zatem
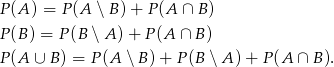
Mamy stąd
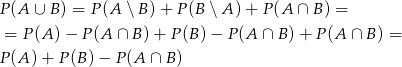
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeśli 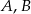 są dowolnymi zdarzeniami przestrzeni
są dowolnymi zdarzeniami przestrzeni 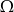 , to
, to 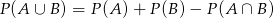 .
.
Jeżeli narysujemy sobie diagram Venna, to widać, że
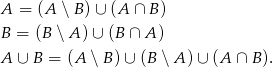
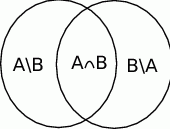
W wszystkich równościach zbiory po prawej stronie są rozłączne, zatem
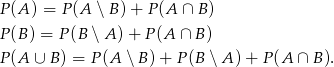
Mamy stąd