/Szkoła średnia/Geometria/Planimetria/Czworokąt/Romb/Pole

Zadanie nr 2564378

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole rombu, w którym długość boku jest równa 13 cm, a długości przekątnych różnią się o 14 cm.

Rozwiązanie

Oznaczmy długości przekątnych rombu przez 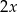2x i 2y .

PIC

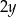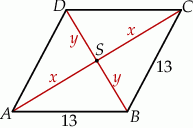
Wiemy zatem, że

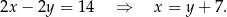
2x − 2y = 14 ⇒ x = y + 7.

Ponieważ przekątne rombu dzielą się na połowy oraz są prostopadłe, trójkąt 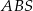ABS jest prostokątny oraz 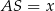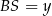AS = x , BS = y . Korzystając z twierdzenia Pitagorasa mamy

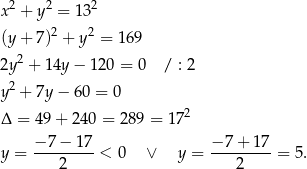
x2 + y2 = 132 (y+ 7)2 + y2 = 169 2 2y + 14y − 120 = 0 / : 2 y2 + 7y − 60 = 0 2 Δ = 49+ 240 = 28 9 = 17 − 7 − 17 − 7+ 17 y = ---------< 0 ∨ y = ---------= 5 . 2 2

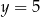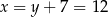Zatem y = 5 i x = y+ 7 = 12 .

Pole rombu jest cztery razy większe od pola trójkąta 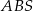ABS (bo wszystkie cztery narysowane trójkąty są przystające), zatem

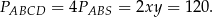
PABCD = 4PABS = 2xy = 120.

 
Odpowiedź: 120

Wersja PDF