/Szkoła średnia/Geometria/Planimetria/Czworokąt/Romb/Pole

Zadanie nr 6329196

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód rombu jest równy 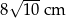√ --- 8 10 cm , a jedna z jego przekątnych jest o 8 cm dłuższa od drugiej. Oblicz pole rombu.

Rozwiązanie

Zaczynamy od rysunku

PIC

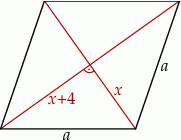
Przekątne w rombie dzielą się na dwie równe części i przecinają pod kątem prostym, więc jeżeli oznaczymy przez 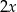2x długość krótszej przekątnej to otrzymamy, że połowa długości dłuższej wynosi

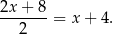
2x-+--8 2 = x + 4.

Wyznaczamy długość boku rombu

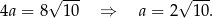
√ --- √ --- 4a = 8 10 ⇒ a = 2 10.

Korzystamy z twierdzenia Pitagorasa żeby wyznaczyć x

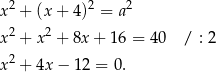
x2 + (x + 4)2 = a 2 2 2 x + x + 8x + 16 = 40 / : 2 x2 + 4x − 12 = 0.

Obliczamy wyznacznik główny i pierwiastki

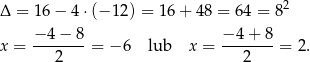
Δ = 16 − 4 ⋅(− 12) = 16+ 48 = 64 = 82 x = −-4-−-8 = − 6 lub x = −-4-+-8 = 2. 2 2

Odrzucamy ujemny wynik i otrzymujemy, że przekątne są równe 4 i 12 cm. Teraz już łatwo policzyć pole

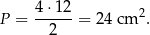
4-⋅12- 2 P = 2 = 24 cm .

 
Odpowiedź: 24 cm 2

Wersja PDF