Zadanie nr 2673813
Gdyby Aleksander Wielki umarł o 5 lat wcześniej, to panowałby przez 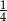 swego życia. Gdyby żył o 9 lat dłużej, to panowałby przez połowę swego życia. Ile lat żył i ile lat panował.
swego życia. Gdyby żył o 9 lat dłużej, to panowałby przez połowę swego życia. Ile lat żył i ile lat panował.
Rozwiązanie
Sposób I
Jeżeli oznaczymy przez  wiek Aleksandra Wielkiego w chwili śmierci, a przez
wiek Aleksandra Wielkiego w chwili śmierci, a przez 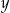 długość jego panowania, to mamy układ równań (liczymy ile lat panował).
długość jego panowania, to mamy układ równań (liczymy ile lat panował).
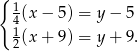
Odejmując od drugiego równania pierwsze (żeby skrócić 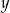 ) mamy
) mamy
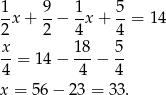
Z pierwszego równania mamy więc
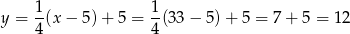
Sposób II
Jeżeli oznaczymy przez  wiek Aleksandra Wielkiego w chwili śmierci to mamy równanie (liczymy na dwa sposoby ile lat panował).
wiek Aleksandra Wielkiego w chwili śmierci to mamy równanie (liczymy na dwa sposoby ile lat panował).
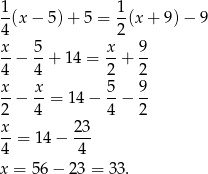
Zatem żył 33 lata, a panował
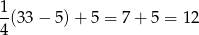
lat.
Odpowiedź: Żył 33 lata, panował przez 12 lat.

