Wykaż, że jeżeli 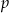 jest liczbą pierwszą większą od 3 to
jest liczbą pierwszą większą od 3 to 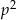 przy dzieleniu przez 24 daje resztę 1.
przy dzieleniu przez 24 daje resztę 1.
/Konkursy
Wykaż, że liczba  jest dla dowolnej liczby naturalnej
jest dla dowolnej liczby naturalnej  kwadratem liczby całkowitej.
kwadratem liczby całkowitej.
Uzasadnij, że równanie 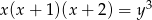 nie ma rozwiązań w liczbach całkowitych dodatnich
nie ma rozwiązań w liczbach całkowitych dodatnich 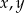 .
.
Do narysowania przedstawionej na rysunku tablicy zawierającej 12 komórek użyto 5 prostych poziomych i 4 pionowych. Jeżeli użyjemy 6 prostych poziomych i 3 pionowych, to otrzymamy tablice o 10 komórkach. Jaką największą liczbę komórek można otrzymać, używając do narysowania tablicy 15 prostych?

A) 56 B) 27 C) 32 D) 40 E) 42
W diagramie obok każda litera oznacza cyfrę, przy czym różne litery oznaczają różne cyfry. Jaka cyfra, z poniżej podanych, kryje się pod literą 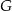 ?
?
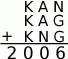
A) 1 B) 2 C) 3 D) 4 E) 5
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
Na różnych prostych równoległych  i
i 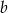 obrano 6 punktów: 4 punkty na prostej
obrano 6 punktów: 4 punkty na prostej  i 2 punkty na prostej
i 2 punkty na prostej 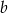 . Ile jest trójkątów, których wszystkie wierzchołki są w wybranych punktach?
. Ile jest trójkątów, których wszystkie wierzchołki są w wybranych punktach?
A) 6 B) 8 C) 12 D) 16 E) 18
Która z liczb jest większa 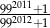 , czy
, czy 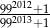 ?
?
Która z liczb jest większa: 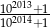 , czy
, czy 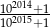 ?
?
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Ktoś zapytał znajomego „Ile masz lat?”. „Teraz mam dwa razy więcej niż ty miałeś gdy ja byłem w twoim wieku. Gdy ty będziesz w moim wieku razem będziemy mieć 63 lata”. Ile lat ma każdy z nich obecnie?
Na bokach 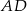 i
i 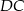 kwadratu
kwadratu 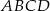 o polu 1 wybrano punkty
o polu 1 wybrano punkty 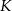 i
i 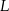 w ten sposób, że
w ten sposób, że 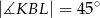 .
.
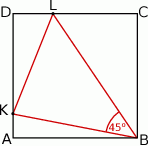
Oblicz odległość punktu 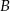 od prostej
od prostej 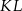 .
.
Dwusieczna 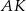 kąta
kąta 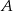 w trójkącie
w trójkącie 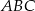 podzieliła ten trójkąt na dwa trójkąty o równych polach. Wówczas trójkąt
podzieliła ten trójkąt na dwa trójkąty o równych polach. Wówczas trójkąt 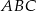 jest na pewno
jest na pewno
A) równoboczny B) równoramienny C) prostokątny D) ostrokątny E) rozwartokątny
Rozwiązaniem równania 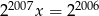 jest liczba
jest liczba
A) 1 B) 2 C) 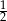 D)
D) 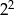 E)
E) 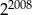
Jeżeli  jest liczbą całkowitą ujemną, to wśród poniższych liczb największą jest:
jest liczbą całkowitą ujemną, to wśród poniższych liczb największą jest:
A) 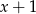 B)
B) 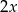 C)
C) 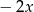 D)
D) 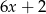 E)
E) 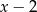
Dwa okręgi są styczne wewnętrznie w punkcie 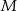 . Cięciwa
. Cięciwa 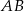 większego okręgu jest styczna do mniejszego okręgu w punkcie
większego okręgu jest styczna do mniejszego okręgu w punkcie 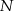 . Oznaczmy przez
. Oznaczmy przez 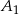 i
i 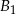 punkty przecięcia prostych
punkty przecięcia prostych 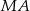 i
i 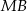 z mniejszym okręgiem. Udowodnić, że
z mniejszym okręgiem. Udowodnić, że
- prosta
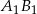 jest równoległa do prostej
jest równoległa do prostej 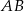 ;
; - prosta
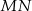 jest dwusieczną kąta
jest dwusieczną kąta 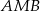 .
.
Jeżeli  i
i 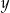 są liczbami całkowitymi o tej własności, że
są liczbami całkowitymi o tej własności, że 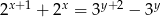 , to
, to  jest równe
jest równe
A) 0 B) 3 C) -1 D) 1 E) 2
Ile zer należy wpisać w miejsce  w zapisie dziesiętnym liczby
w zapisie dziesiętnym liczby 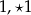 , aby liczba ta była mniejsza niż
, aby liczba ta była mniejsza niż 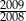 i jednocześnie większa niż
i jednocześnie większa niż 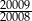 ?
?
A) 1 B) 2 C) 3 D) 4 E) 5
Na rysunku obok brzegi zaznaczonych kwadratów utworzone są przez części odcinka 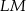 o długości 24 cm i przez odcinki łamanej
o długości 24 cm i przez odcinki łamanej 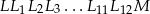 . Ile jest równa długość łamanej
. Ile jest równa długość łamanej 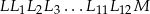 ?
?
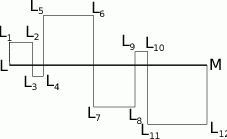
A) 106cm B) 96cm C) 72cm D) 56cm E) 48cm
W trapezie 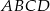 podstawa
podstawa 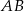 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 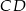 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 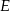 , a proste zawierające ramiona
, a proste zawierające ramiona 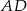 i
i 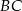 przecinają się w punkcie
przecinają się w punkcie 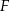 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 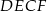 do pola trapezu
do pola trapezu 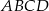 .
.
Samochód ciężarowy, jadąc ze stałą prędkością, przebył drogę z miasta 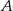 do miasta
do miasta 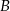 w czasie 1 godziny i 30 minut i drogę z miasta
w czasie 1 godziny i 30 minut i drogę z miasta 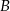 do miasta
do miasta 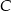 w czasie 1 godziny. Tę samą trasę pokonywał, również ze stałą prędkością, samochód osobowy, który z miasta
w czasie 1 godziny. Tę samą trasę pokonywał, również ze stałą prędkością, samochód osobowy, który z miasta 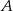 do miasta
do miasta 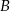 jechał 1 godzinę. Ile czasu jechał ten samochód z miasta
jechał 1 godzinę. Ile czasu jechał ten samochód z miasta 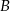 do miasta
do miasta 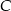 ?
?
A) 45 minut B) 40 minut C) 35 minut D) 30 minut E) 90 minut

