Niech 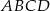 będzie kwadratem o boku 12 cm. Punkty
będzie kwadratem o boku 12 cm. Punkty 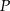 ,
, 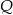 ,
, 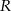 są odpowiednio środkami boków
są odpowiednio środkami boków 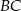 ,
, 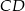 ,
, 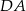 (rysunek obok). Pole zacieniowanego czworokąta jest równe
(rysunek obok). Pole zacieniowanego czworokąta jest równe
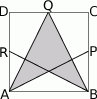
A) 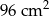 B)
B) 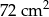 C)
C) 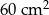 D)
D) 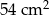 E)
E) 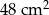
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Niech 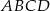 będzie kwadratem o boku 12 cm. Punkty
będzie kwadratem o boku 12 cm. Punkty 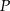 ,
, 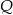 ,
, 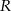 są odpowiednio środkami boków
są odpowiednio środkami boków 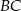 ,
, 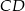 ,
, 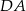 (rysunek obok). Pole zacieniowanego czworokąta jest równe
(rysunek obok). Pole zacieniowanego czworokąta jest równe

A) 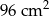 B)
B) 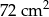 C)
C) 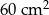 D)
D) 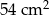 E)
E) 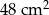
Na rysunku przedstawiono kwadratową tablicę 4x4 składającą się z 16 kwadracików jednostkowych. Ile jest równa największa możliwa liczba przekątnych, jakie można poprowadzić w tych kwadracikach jednostkowych w ten sposób, aby żadne dwie z nich nie przecinały się, ani nie miały wspólnych końców?
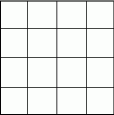
A) 8 B) 9 C) 10 D) 11 E) 12
W trójkącie ostrokątnym 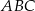 prawdziwa jest równość
prawdziwa jest równość 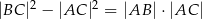 . Wykaż, że kąt
. Wykaż, że kąt 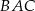 jest dwa razy większy od kąta
jest dwa razy większy od kąta 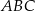 .
.
Wyznacz wszystkie liczby naturalne  , dla których
, dla których 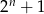 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Daniel ma 9 monet, każda o nominale 2 złotych, zaś jego siostra Ania ma 8 monet, każda o nominale 5 złotych. Jaką najmniejszą liczbę monet muszą oni między sobą wymienić, aby mieć równe kwoty?
A) 4 B) 5 C) 8 D) 12 E) Nie da się tego zrobić
Jaka jest najmniejsza liczba całkowita  , dla której liczba
, dla której liczba
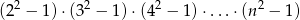
jest kwadratem liczby całkowitej?
A) 6 B) 8 C) 16 D) 27 E) Inna odpowiedź
Przekątne czworokąta wypukłego 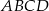 przecinają się w punkcie
przecinają się w punkcie 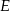 . Wiadomo, że trójkąty
. Wiadomo, że trójkąty 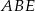 i
i 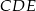 mają równe pola, długość boku
mają równe pola, długość boku 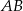 jest równa 4, a przekątna
jest równa 4, a przekątna 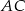 jest zawarta w dwusiecznej kąta
jest zawarta w dwusiecznej kąta 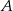 . Oblicz długość boku
. Oblicz długość boku 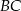 .
.
Wykaż, że jeżeli 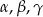 są kątami trójkąta, to
są kątami trójkąta, to
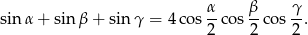
W polach szachownicy 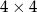 chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
A) 7 B) 10 C) 14 D) 18 E) 28
Pewnego dnia postawiłem dla psów miskę z psimi ciasteczkami. Najpierw przyszedł najstarszy pies i zjadł połowę ciasteczek, i jeszcze jedno. Potem przyszedł drugi pies zjadł połowę tego, co znalazł i jeszcze jedno ciasteczko. Potem przyszedł trzeci pies i także zjadł połowę tego, co znalazł i jeszcze jedno ciasteczko. Wreszcie przyszedł czwarty najmniejszy piesek i zjadł połowę tego, co zostało, i jeszcze jedno ciasteczko, wtedy ciasteczka się skończyły. Ile ich było na początku w misce?
W czworokącie 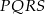 mamy
mamy 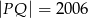 ,
, 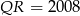 ,
, 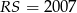 ,
, 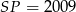 . Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż
. Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż 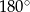 ?
?
A) 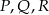 B)
B) 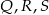 C)
C) 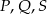 D)
D) 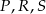 E)
E) 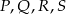
Wyznacz długości boków trójkąta wiedząc, że są one kolejnymi liczbami naturalnymi zaś największy kąt jest dwa razy większy od kąta najmniejszego.
Udowodnij, że dla dowolnych kątów 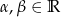 prawdziwe są tożsamości
prawdziwe są tożsamości
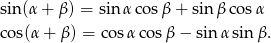
Przez środek 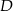 przyprostokątnej
przyprostokątnej 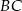 trójkąta prostokątnego
trójkąta prostokątnego 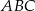 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 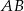 . Prosta ta przecina proste
. Prosta ta przecina proste 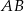 i
i 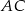 odpowiednio w punktach
odpowiednio w punktach 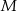 i
i 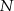 . Wykaż, że
. Wykaż, że 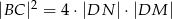 .
.
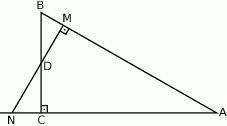
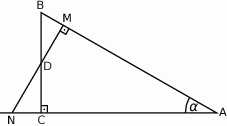
Przez środek 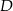 przyprostokątnej
przyprostokątnej 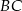 trójkąta prostokątnego
trójkąta prostokątnego 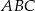 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 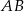 . Prosta ta przecina proste
. Prosta ta przecina proste 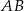 i
i 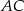 odpowiednio w punktach
odpowiednio w punktach 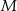 i
i 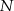 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 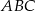 i
i 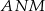 jest równa
jest równa 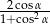 .
.
Wykaż, że jeżeli 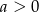 i
i 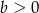 oraz
oraz 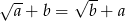 to
to 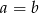 lub
lub 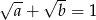 .
.
Wykaż, że jeżeli liczby dodatnie  i
i 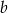 spełniają warunek
spełniają warunek
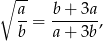
to 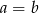 .
.
W pokoju znajdowała się pewna liczba osób. Ich średni wiek równy był liczbie osób znajdujących się w pokoju. Gdy do pokoju wszedł 29 letni człowiek, okazało się, że średni wiek był równy liczbie osób w pokoju. Ile osób znajdowało się na początku w pokoju?
A) 14 B) 15 C) 16 D) 17 E) 18
Zosia, Marysia i Ania weszły do klasy gdzie na wielkim transparencie były zapisane liczby od 1 do 7777. Zosia zakreśliła na różowo wszystkie liczby podzielne przez 3. Marysia zakreśliła na zielono wszystkie liczby podzielne przez 4. Ania zakreśliła na fioletowo wszystkie liczby podzielne przez 6. Ile liczb zostało zakreślonych dwukrotnie (bez względu na kolor)?
Rakietą podróżowała grupa kosmitów. Każdy z nich ubrany był w kombinezon w jednym z trzech kolorów: zielonym, pomarańczowym, niebieskim. Każdy ubrany na zielono kosmita miał dwa czułki, każdy ubrany na pomarańczowo miał trzy czułki, a każdy ubrany na niebiesko miał pięć czułków. Wszystkich kosmitów ubranych na zielono było tylu, ilu ubranych na pomarańczowo, a ubranych na niebiesko było o 10 więcej niż ubranych na zielono. Wszyscy razem mieli 250 czułków. Ilu ubranych na niebiesko kosmitów podróżowało rakietą?
A) 15 B) 20 C) 25 D) 30 E) 40
Trzy koła o promieniu 1 są parami styczne zewnętrznie. Oblicz pole obszaru zawartego między tymi kołami.
Ramiona kąta o mierze 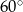 przecięto prostą
przecięto prostą 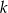 prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej
prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej 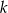 . Oblicz stosunek pól tych kół.
. Oblicz stosunek pól tych kół.
