Wykaż, że jeżeli liczby całkowite  i
i 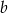 spełniają równanie
spełniają równanie
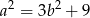
to liczba 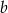 dzieli się przez 3, a liczba
dzieli się przez 3, a liczba  nie dzieli się przez 9.
nie dzieli się przez 9.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli liczby całkowite  i
i 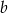 spełniają równanie
spełniają równanie
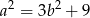
to liczba 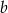 dzieli się przez 3, a liczba
dzieli się przez 3, a liczba  nie dzieli się przez 9.
nie dzieli się przez 9.
Prostokąt, który widzimy obok na rysunku, podzielono na 7 kwadratów. Bok każdego z zacieniowanych kwadratów ma długość 8. Jaką długość ma bok dużego białego kwadratu?

A) 16 B) 18 C) 20 D) 24 E) 30
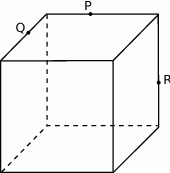
Narysuj przekrój równoległościanu płaszczyzną 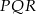 .
.
Jacek powiedział, że 25% jego książek to opowiadania, a 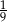 to poezje. Wiadomo, że ma on co najmniej 50 książek, ale nie więcej niż 100. Ile książek ma Jacek?
to poezje. Wiadomo, że ma on co najmniej 50 książek, ale nie więcej niż 100. Ile książek ma Jacek?
A) 50 B) 56 C) 64 D) 72 E) 93
W kryptogramie różnym literom odpowiadają różne cyfry. Podaj rozwiązanie.
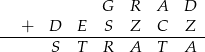
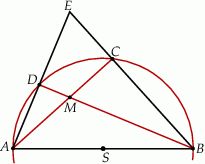
Na okręgu o środku 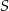 wybrano punkty
wybrano punkty 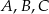 i
i 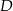 w ten sposób, że prosta
w ten sposób, że prosta 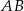 zawiera punkt
zawiera punkt 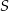 , a proste
, a proste 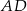 i
i 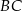 przecinają się w punkcie
przecinają się w punkcie 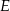 . Punkt
. Punkt 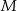 jest punktem wspólnym prostych
jest punktem wspólnym prostych 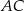 i
i 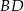 . Wykaż, że proste
. Wykaż, że proste 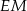 i
i 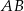 są prostopadłe.
są prostopadłe.
Dla jakich  należących do zbioru liczb naturalnych liczba
należących do zbioru liczb naturalnych liczba 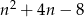 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Rozwiąż nierówność 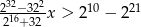 . Podaj najmniejszą liczbę całkowitą spełniającą tę nierówność.
. Podaj najmniejszą liczbę całkowitą spełniającą tę nierówność.
Ile jest liczb naturalnych, o sumie cyfr równej 10, w których zapisie mogą występować tylko cyfry 1 lub 3?
A) 28 B) 34 C) 35 D) 55 E) 56
Dodatnia liczba naturalna  jest najmniejszą liczbą taką, że
jest najmniejszą liczbą taką, że 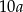 jest kwadratem pewnej liczby naturalnej, a
jest kwadratem pewnej liczby naturalnej, a 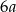 sześcianem pewnej liczby naturalnej. Ile różnych dzielników ma liczba
sześcianem pewnej liczby naturalnej. Ile różnych dzielników ma liczba  ?
?
A) 30 B) 40 C) 54 D) 72 E) 96
Czworo przyjaciół zamierza na przyjęciu dać sobie nawzajem prezenty w taki sposób, że każdy da tylko jednej osobie prezent, i każdy otrzyma prezent tylko od jednej osoby (oczywiście nikt nie daje prezentu sobie). Na ile sposobów można to zrobić?
A) 9 B) 10 C) 12 D) 16 E) 24
Udowodnij, że jeżeli 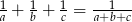 to
to 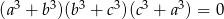 .
.
Na bokach 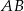 ,
, 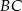 i
i 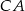 trójkąta
trójkąta 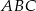 wybrano odpowiednio punkty
wybrano odpowiednio punkty 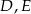 i
i 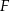 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 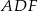 ,
, 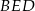 i
i 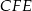 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Oblicz długość boku rombu wiedząc, że prosta poprowadzona przez jeden z jego wierzchołków odcina na przedłużeniach dwóch jego boków odcinki o długościach 4 i 9.
Ile czterocyfrowych liczb, których wszystkie cztery cyfry są różne, dzieli się przez 2006?
A) 1 B) 2 C) 3 D) 4 E) 5
Dwa wzajemnie styczne okręgi o równych promieniach mają środki w dwóch przeciwległych wierzchołkach kwadratu. Kolejne dwa okręgi, o środkach w pozostałych wierzchołkach kwadratu, są styczne zewnętrznie do każdego z dwóch poprzednich okręgów (patrz rysunek). Ile razy promień większego okręgu jest większy od promienia mniejszego okręgu?
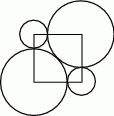
A) 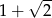 B)
B) 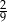 C)
C) 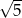 D)
D) 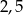 E)
E) 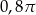
Kangur wymyślił nowe działanie  w zbiorze liczb naturalnych dodatnich. Podał kilka przykładów:
w zbiorze liczb naturalnych dodatnich. Podał kilka przykładów: 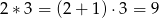 ;
; 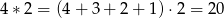 ;
; 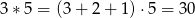 . Jaki jest wynik działania
. Jaki jest wynik działania 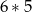 ?
?
A) 30 B) 90 C) 105 D) 210 E) 315
Udowodnij, że dla dowolnych liczb 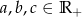 zachodzi nierówność
zachodzi nierówność
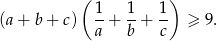
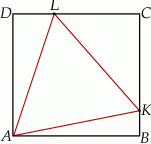
W prostokąt 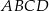 wpisany jest trójkąt równoboczny
wpisany jest trójkąt równoboczny 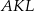 (patrz rysunek). Wierzchołek
(patrz rysunek). Wierzchołek 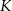 leży na boku
leży na boku 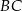 (
(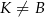 i
i 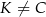 ), wierzchołek
), wierzchołek 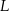 leży na boku
leży na boku 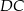 (
(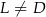 i
i 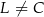 ). Udowodnij, że pole powierzchni trójkąta
). Udowodnij, że pole powierzchni trójkąta 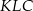 równe jest sumie pól trójkątów
równe jest sumie pól trójkątów 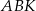 i
i 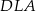 .
.
Na okręgu wybrano takich pięć różnych punktów: 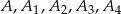 , że
, że
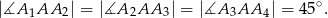
Udowodnij, że punkty 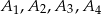 są wierzchołkami kwadratu.
są wierzchołkami kwadratu.
