Dany jest prostokąt 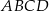 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 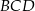 jest styczny do przekątnej
jest styczny do przekątnej 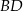 w punkcie
w punkcie 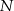 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 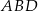 jest styczny do boku
jest styczny do boku 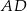 w punkcie
w punkcie 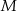 , a środek
, a środek 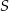 tego okręgu leży na odcinku
tego okręgu leży na odcinku 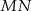 , jak na rysunku.
, jak na rysunku.
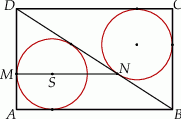
Wykaż, że 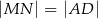 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest prostokąt 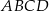 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 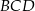 jest styczny do przekątnej
jest styczny do przekątnej 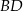 w punkcie
w punkcie 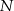 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 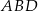 jest styczny do boku
jest styczny do boku 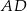 w punkcie
w punkcie 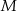 , a środek
, a środek 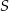 tego okręgu leży na odcinku
tego okręgu leży na odcinku 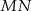 , jak na rysunku.
, jak na rysunku.

Wykaż, że 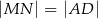 .
.
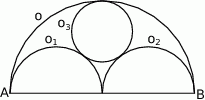
W półkolu  o średnicy
o średnicy 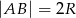 narysowano dwa przystające i zewnętrznie styczne półkola
narysowano dwa przystające i zewnętrznie styczne półkola 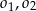 , których środki leżą na odcinku
, których środki leżą na odcinku 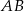 , i które są wewnętrznie styczne do półkola
, i które są wewnętrznie styczne do półkola  . Oblicz promień okręgu
. Oblicz promień okręgu 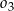 , który jest styczny do
, który jest styczny do 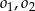 i
i  .
.
Na ile sposobów można zapłacić 250 zł monetami 1,2 i 5 złotowymi?
Jeżeli 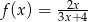 oraz
oraz 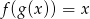 , to
, to
A) 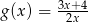 B)
B) 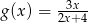 C)
C) 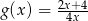 D)
D) 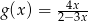 E)
E) 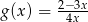
W trójkącie prostokątnym 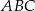 o kącie prostym w wierzchołku
o kącie prostym w wierzchołku 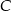 obrano taki punkt
obrano taki punkt 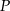 , że pola trójkątów
, że pola trójkątów 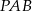 ,
, 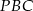 i
i 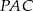 są równe. Oblicz długość odcinka
są równe. Oblicz długość odcinka 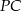 , wiedząc, że
, wiedząc, że 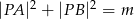 .
.
W grze losowej wygrywają kupony o numerach co najmniej 5-cyfrowych, w których co najwyżej 3 cyfry są większe od 2. Ile jest kuponów wygrywających wśród kuponów o numerach 1022, 22222, 102334, 213343, 3042531?
A) 1 B) 2 C) 3 D) 4 E) 5
Dana jest kula o promieniu 3 i o środku w początku układu współrzędnych. Ile punktów na powierzchni tej kuli ma wszystkie współrzędne całkowite?
A) 30 B) 24 C) 12 D) 6 E) 3
Czarek myśli, że każdy trójkąt równoramienny jest ostrokątny. Który z poniższych przykładów pokazuje, że Czarek nie ma racji?

W trójkącie 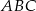 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku 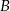 jest równa
jest równa 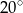 , a miara kąta wewnętrznego przy wierzchołku
, a miara kąta wewnętrznego przy wierzchołku 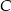 jest równa
jest równa 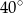 . Ponadto długość dwusiecznej kąta przy wierzchołku
. Ponadto długość dwusiecznej kąta przy wierzchołku 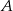 jest równa 2. Ile wynosi różnica
jest równa 2. Ile wynosi różnica 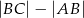 ?
?
A) 1 B) 1,5 C) 2 D) 4 E) Nie można jej jednoznacznie wyznaczyć.
Znajdź wszystkie liczby naturalne  takie, że liczba
takie, że liczba 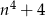 jest liczbą pierwszą.
jest liczbą pierwszą.
Punkt 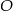 jest środkiem pięciokąta foremnego. Jaką częścią pięciokąta jest zacieniowany obszar?
jest środkiem pięciokąta foremnego. Jaką częścią pięciokąta jest zacieniowany obszar?
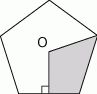
A) 10% B) 20% C) 25% D) 30% E) 40%
Wódz indiański wysłał trzech zwiadowców na zachód, północ i wschód. Każdy z nich oddalił się o 5 km od obozu i miał w zasięgu wzroku teren o promieniu 5 km.
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
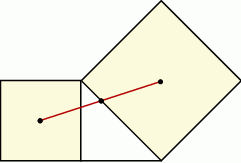
W prostokącie 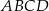 wierzchołek
wierzchołek 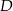 połączono odcinkami ze środkami
połączono odcinkami ze środkami 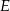 i
i 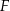 boków
boków 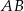 i
i 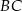 , zaś
, zaś 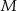 i
i 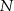 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 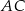 .
.
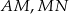 i
i 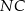 są jednakowej długości.
są jednakowej długości. 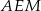 i
i 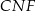 mają równe pola.
mają równe pola.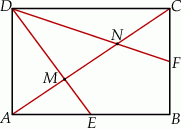
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 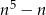 jest podzielna przez 30.
jest podzielna przez 30.
Znajdź wszystkie funkcje 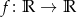 , dla których zachodzi równość
, dla których zachodzi równość 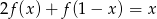 .
.
Statek wycieczkowy, płynąc z prądem rzeki, pokonuje trasę z miasta 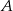 do miasta
do miasta 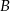 w ciągu dwóch godzin, natomiast z powrotem płynie o pół godziny dłużej. Ile czasu będzie płynąć tratwa z miasta
w ciągu dwóch godzin, natomiast z powrotem płynie o pół godziny dłużej. Ile czasu będzie płynąć tratwa z miasta 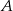 do miasta
do miasta 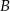 ?
?
3–piramida to stos utworzony z trzech warstw kul przedstawionych na rysunku. W ten sam sposób otrzymujemy 4–piramidę, 5-piramidę, itd.
Gdy usuniemy wszystkie kule „ścian bocznych” i „podstawy” 8-piramidy, to otrzymamy
![]()
A) 3–piramidę B) 4–piramidę C) 5–piramidę D) 6–piramidę E) 7–piramidę
Wykaż, że jeżeli 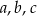 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 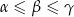 to
to 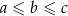 .
.
Na okręgu rozmieszczono liczby: 1,2,3. Pomiędzy każde dwie sąsiednie liczby wpisano ich sumy, otrzymując na okręgu sześć liczb 1,3,2,5,3,4. Operację wpisywania sum liczb sąsiednich powtórzono jeszcze trzy razy. W rezultacie otrzymano na okręgu 48 liczb. Ile wynosi ich suma?
A) 162 B) 1458 C) 486 D) 144 E) 210
