Zadanie nr 6265321
Wykaż, że jeżeli 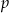 jest liczbą pierwszą większą od 3 to
jest liczbą pierwszą większą od 3 to 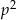 przy dzieleniu przez 24 daje resztę 1.
przy dzieleniu przez 24 daje resztę 1.
Rozwiązanie
Sposób I
Musimy pokazać, że
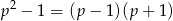
dzieli się przez 24, czyli, że dzieli się przez 8 i przez 3. Ponieważ 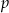 jest liczbą pierwszą większą od 3, więc nie dzieli się przez 3. Zatem przez 3 dzieli się jedna z liczb
jest liczbą pierwszą większą od 3, więc nie dzieli się przez 3. Zatem przez 3 dzieli się jedna z liczb 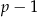 lub
lub 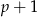 , czyli
, czyli 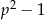 dzieli się przez 3.
dzieli się przez 3.
Pozostało wykazać, że 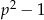 dzieli się przez 8. Liczba
dzieli się przez 8. Liczba 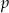 jest nieparzysta, więc jest postaci
jest nieparzysta, więc jest postaci 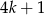 lub
lub 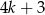 (bo nie może być postaci
(bo nie może być postaci 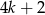 ani
ani 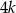 ). Zatem odpowiednio
). Zatem odpowiednio
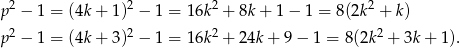
W obu przypadkach otrzymujemy liczbę podzielną przez 8.
Sposób II
Tak jak wyżej zauważamy, że liczba 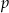 nie dzieli się przez 2 ani przez 3. Zatem jest postaci
nie dzieli się przez 2 ani przez 3. Zatem jest postaci 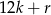 , gdzie
, gdzie 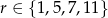 . Mamy zatem
. Mamy zatem
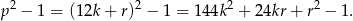
Podstawiając za  liczby 1,5,7,11 łatwo sprawdzić, że w każdym przypadku
liczby 1,5,7,11 łatwo sprawdzić, że w każdym przypadku 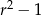 dzieli się przez 24.
dzieli się przez 24.

