/Konkursy

Zadanie nr 6600626

Dodaj do ulubionych
Dodaj do rozwiązanych

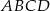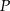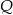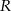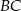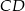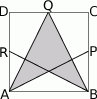
Niech ABCD będzie kwadratem o boku 12 cm. Punkty P , Q , R są odpowiednio środkami boków 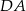BC , CD , DA (rysunek obok). Pole zacieniowanego czworokąta jest równe

PIC

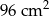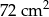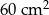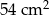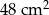
A) 96 cm 2 B) 72 cm 2 C) 60 cm 2 D) 54 cm 2 E) 48 cm 2

Rozwiązanie

Szukane pole jest równe różnicy

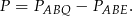
P = PABQ − PABE .

PIC

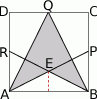
Wystarczy teraz zauważyć, że 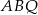ABQ ma pole równe połowie pola kwadratu, a 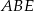ABE jednej ósmej pola kwadratu (bo wysokość jest równa czwartej częsci boku kwadratu). Mamy więc

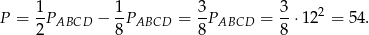
1- 1- 3- 3- 2 P = 2PABCD − 8 PABCD = 8PABCD = 8 ⋅12 = 5 4.

 
Odpowiedź: D

Wersja PDF